ACTUS SYSTÉMŮ PRVOČÍSELNÝCH MATIC

ACTUS je mnou zvolený výraz pro určitý druh operací které změní obecnou SYMETRICKOU matici typu C(n=k^2,2,k) na sytém NESYMETRICKÝ. Při tom se zvýší C(n,2,k) na C(n+k+1,2,k+1).

Podstata je celkem velice jednoduchá, ale já se domnívám, že je to také jedna z cest která má potenciál vysvětlit algoritmus výskytu některých, nebo i všech prvočísel.

Základní myšlenka (dogma) je postavena na systémech čistě prvočíselných a tím pádem také SYMETRICKÝCH matic. Ve skutečnosti ukážeme, že se to týká ještě nejméně čtverců z mocnin prvočísel a pravděpodobně také lichých čísel daných součinem dvou prvočísel – pak jde už o čísla složená. [u]Jen velmi opatrně naznačím, že by se mohlo jednat o systémy p-adických množin (množiny složené ze součinu čísel s kongruencí prvočíselné modulo). Tyto systémy by zřejmě nemusely být nutně symetrické.[/u]

ACTUS 1

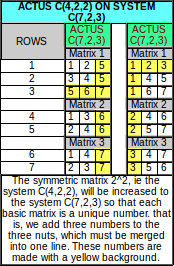
Tabulka názorně popisuje vznik nesymetrického systému dvojic. Ze systému C(4,2,2) = Combin(4;2) = 6 dvojic, proto vyjadřuje 3 matice z nichž je první souřadnice a zbylé dvě tvoří prostorovou krychli 2^3 prvků (p)^0.

Přidali jsme každému sloupci další číslo. Z toho plyne : 3 sloupce = přidána 3 čísla – jedno vždy celému sloupci. Tím vznikly z dvojic (k=2) trojice (k=3) a museli jsme ještě přidat řádek, který přidaná čísla sváže tak aby mezi sebou také utvořili dvojice.

Actus je proveden hned dvěma způsoby. První je vlevo a ukazuje naturalisticky přidání tří čísel „od konce“. Tedy k číslům 1, 2, 3, 4 přidáváme ještě  čísla 5, 6 a 7. Ta jsou větší a proto patří logicky na poslední místa ve trojicích. Druhý způsob není takto „logický“ ale je „hezčí“. Přes to má svou logiku která spočívá ve skutečnosti že přidávat můžeme také „od začátku“. V takovém případě se přidávají čísla od 1 do (k+1). Znamená to jen primitivně substitucí zvýšit hodnoty původního základu o přidaný počet prvků. Proto máme místo jedničky čtyřku, místo dvojky pětku, místo trojky šestku a místo čtyřky sedmičku.

ACTUS 2

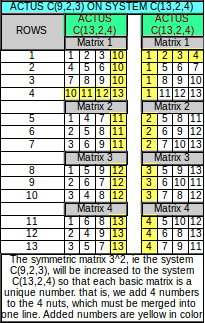
Zde vidíme že ACTUS vytváří sice nesymetrické systémy, ale PRVOČÍSEL. V případě prvém jsme skočili ze základu čísla 4 (2^2) na základ číslo 7. Přeskočili jsme tak prvočísla 3 a 5. Ve druhém případě jsme ze základu 9 (3^2) skočili na číslo 13 ale přeskočili jsme prvočíslo 11.

Další zajímavostí je, že ACTUS má stejný počet řádků v maticích jako je základ počtu dvojic.

Actus na číslo 7 má 7 řádků trojic v nichž jsou obsaženy všechny dvojice celku 7. Konkrétně COMBIN(7;2) = 21 dvojic a řádek trojice obsahuje COMBIN(3;2) = 3 dvojice. Tato čísla jsou soudělná : 21/3 = 7.

Totéž ukazuje ACTUS na číslo 13. Také obsahuje 13 řádků, nyní ale čtyř-čísel, které opět obsahují všechny dvojice z celku 13. Konkrétně COMBIN(13;2) = 78 dvojic a řádek čtveřice obsahuje COMBIN(4;2) = 6 dvojic. Tato čísla jsou soudělná : 78/6 = 13.

Předpokládaný význam algoritmu ACTUS

Actus vypadá, že je jakýmsi doplňkem k postupu Sophie Germain, který popisuje řadu prvočísel 2, 3, 5, 11, 23, 29, 41, 53, 83, 113, 131 a tak dál. Actus je více podobný s Marsenne prvočísly. Správně bychom měli hovořit o konstruktorech prvočísel, ale Actus je algoritmem který slouží původně k jinému účelu, nežli ke konstrukci řady prvočísel a není předložen ve formě konstruktoru.

ACTUS 3

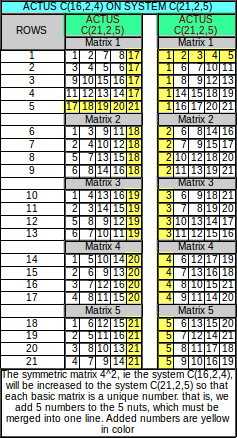
Tento popis algoritmu už přesahuje rámec prvočíselných rozšíření. Číslo 21 je dáno součinem 3×7 a jedná se o číslo složené ze dvou prvočísel. Základem je symetrický systém sudé mocniny 4^2 kterou můžeme popsat také jako 2^4. Zde se zřejmě projevuje v jiné podobě skutečnost, že pro číslo 4 si je součet i součin roven (2+2 = 2*2).

Je to zatím jediný symetrický sudý systém mimo dvojky, ale může být také posledním který lze sestrojit [u]zcela[/u] v dobrém uspořádání. Já jsem v tomto smyslu spíš skeptický, ale doufám že to není pravda. Ukážeme si dál proč si to myslím a proč doufám. Pro pesimistický předpoklad svědčí problematika Latinských čtverců.

ACTUS 4

Toto rozšíření je opět na úroveň prvočísla – konkrétně 31. Nyní „přeskakujeme“ mnoho prvočísel. Postup, tedy algoritmus pro ACTUS je stále stejný, ale nabízí se určitá možnost. Je pravděpodobné, že všechna prvočísla lze dovodit podobným algoritmem. Je celkem jisté že nemůže být na bázi symetrických systémů dvojic. Může být ale nesymetrickým systémem v základu který se rozšíří podobně jako systémy symetrické.

ACTUS 5

Na tomto systému je zajímavé, že základní symetrický systém vznikl jakoby z Actus 1 který vytvořil sedmičkový systém. Zde se sedmička dostává jako druhá mocnina do počtu možných (n) pro COMBIN(n=49;k=7). Systém je rozšířen o číslo 8 = (k+1).

Bohu žel rozšíření není na prvočíslo, ale je to také zajímavé. 57 = 3*19. Mohlo by se zdát, že je to náhoda. Tuto nemohu vyloučit, ale upozorňuji, že trojka se vyskytovala v původním ACTUSu číslo 1 právě v souvislosti se sedmičkou. Podíl nás „jakoby“ vrací k prvočíslu 19, které jsme přeskočili protože je mezi ACTUSy 13 a 21 (respektive mezi čistě prvočíselnými 13 a 31).

ACTUS 6

Tento systém je také dost odlišný už od samého základu, který musel být sestrojen upraveným algoritmem. Přestože 91 není prvočíslo je to součin 7*13. Tato prvočísla jsou dána jako ACTUS 1 (7) a ACTUS 2 (13).

Myslím, že lze vyjádřit vnitřní závislosti na prvočíslech nižší úrovně. Zde vidíme závislost na dvou actusech ale základ symetrické množiny (81) je dán jako 9^2, nebo 3^4.

Porovnání konstruktorů

Dříve jsme si ukázali k čemu a jak funguje ACTUS. Nyní ukážeme tabulku kde porovnáme konstruktory mezi které zahrnuji také ACTUS ačkoliv nejde vysloveně o konstruktor. Pouze by mělo být demonstrováno, že se může jednat o určitý typ konstruktoru, nebo možnost sestrojit na této podstatě skutečný konstruktor.

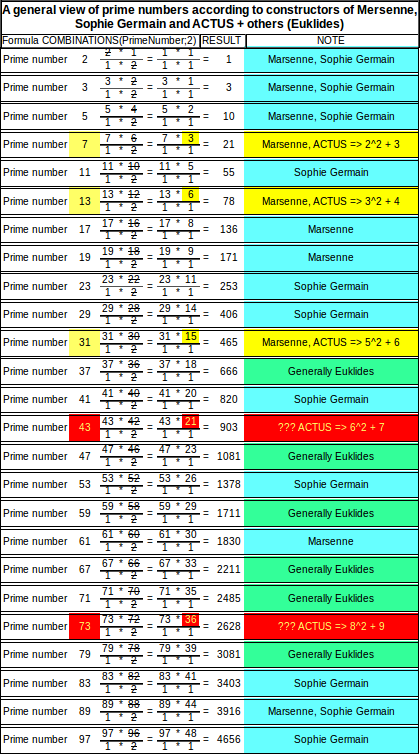
Actus sám o sobě se pohybuje v relaci mezi čtverci prvočísel a za určitých předpokladů lze odvozovat prvočísla. Nejen tedy směrem nahoru jak ukazují žluté podklady, ale i směrem dolů. Domnívám se, že počet řádků ACTUS je v relaci součinů prvočísel pokud není tento počet přímo prvočíslem.

Na pravé straně jsou poznámky které se týkají „bezpečných“ prvočísel na principu konstruktoru Sophie Germain, Mersennova konstruktoru, nebo poznámka že jde o obecně známé prvočíslo. To je zavedeno poznámkou že jde o obecné Euklidovské řešení. Přestože existují další metody které tuto oblast také překrývají.

V tabulce je zavedena predikce ACTUS konstruktoru plynoucího ze sudých čtverců – konkrétně Latinské čtverce, které jsou problematické samy o sobě. Přes to doufám, že se řešení najde v rámci dobře uspořádaných symetrických systémech. Je možné se také odvolat na řešení pomocí vyššího čtverce prvočísel.

Přes to lze zřejmě použít teoretické (prakticky fabulované) systémy symetrických matic druhých mocnin sudých čísel. Analyticky takové systémy najdeme a skutečnost že je nelze prakticky zkonstruovat zde nemusí hrát žádnou úlohu. To se týká jen KONSTRUKTIVNÍ KOMBINATORIKY, nebo LINEÁRNÍ ALGEBRY. Konstruktoru se to přímo netýká. Respektive můžeme problém postavit na úroveň p-adic prostorů. Existuje teorie, že se každé sudé číslo dá rozložit na součet lichých čísel, respektive prvočísel. Tento problém je také jedním z důvodů proč doufám, že se najde algoritmus pro sudé symetrické systémy.

Součet lichých čísel, respektive prvočísel do sudého čísla je dán z druhé třídy PN(n,2) a větší sudá čísla budou mít více „vhodných“ rozkladů. To je problém analýzy a pochopení terminologie posloupností tříd PN jako rozpad na intervaly matematického času. Součet totiž reprezentuje „nesoučasnost“. Naproti tomu součin reprezentuje „současnost“. To jsou ale v této fázi výkladu vágní pojmy. Předbíhám ale k problematice se vrátíme v příslušných kapitolách.

Závěr kapitoly

ACTUS je konstrukční metoda která má pouze pozitivní smysl výrazu. [u]Neexistuje negativní actus (zmenšení systému)[/u] podobným způsobem jak je systém zvyšován.

Celkem se dá pochopit že jsme začali na druhé mocnině čísla 2 a to je první prvočíslo a ještě ke všemu sudé. Jednička není prvočíslem což je odůvodněno klasickou teorií. Pochopíme proto že z této množiny se nedá ubírat směrem dolů. ACTUS je příslušný jen k maticím systémů dvojic směrem nahoru. Každá symetricky a dobře uspořádaná množina dvojic má svůj vlastní ACTUS.

Existuje jiný princip snižování obsahu v rámci symetrických matic a bude zřejmě velice frekventovaný. Všechna čísla lze řešit nejblíže vyšší matici prvočísla. Proto se KONSTRUKTIVNÍ KOMBINATORIKA pohybuje mezi čtverci prvočísel kde vznikají nesymetrické, ale zaručené systémy rozkladů.

Tento závěr už musíme označit jako určitý úvod k obdobě známé teorie USPOŘÁDANÝCH MNOŽIN. Jistě jste zaznamenali tučně zvýrazněné výrazy v podobě „dobře uspořádané (ných)“ systémů…. Jde pouze o výrazovou shodu, protože z pohledu potřeb kombinatorických konstrukcí jsou pojmy jako „poset“ velmi vágní a nic neříkající slova. Jde spíš o přání nežli o validní tvrzení. Jednoduše klasická teorie USPOŘÁDANÝCH MNOŽIN nemá prostředky potřebné pro konstrukce. Proto se od této teorie distancuji – není dost silná pro potřeby této teorie. Otestujte pomocí výroků zmíněné teorie popsat skutečnost rozkladů matic čísla 9, 16, 25 a vyšších. V této teorii je potřebné zejména určit jak „dobře uspořádat“ a také jakým nástrojem. Mimo toho potřebujeme znát základní skutečnost – totiž zda lze skutečně předpokládaným způsobem množinu uspořádat. Nic z toho uvedená teorie USPOŘÁDANÝCH MNOŽIN neumí ani vyjádřit, natož potom validně určit.