Pojem „Přirozená množina“ je v současné době neznámý. Setkáme se s podobnými výrazy, zejména „množina přirozených čísel“, což není totéž. Pojem jsem odvodil při výpočtech pomocí rozšířeného hypergeometrického rozdělení jevu pravděpodobnosti. Pojem přirozená množina se proto vztahuje mimo kombinatoriky zejména k teoriím pravděpodobnosti a statistiky.

Základní teorie se týká diskrétních množin, které mají počet všech možných n = k². Pro spojité (kontinuální) množiny platí vztah k = sqrt(n).

Z tohoto důvodu můžeme provádět převody mezi diskrétními a kontinuálními množinami, respektive D/K a opačně K/D aproximace pomocí relativních četností.

Přirozená množina je proto definována jako diskrétní k a kontinuální (spojité) n, což definujeme podle důkazu „Rozvoj přirozené množiny“. Důkazem je nativní odvození z PN(n).

Rozvoj přirozené množiny

Jedná se o nativní odvozování pro potřeby výpočtů. Potřebujeme zjistit do kolika různých podmnožin lze rozdělit dané k. Takový výpočet existuje v rámci „Partiton“, respektive původním pojmem Partition Numerorum (PN) z celku n možných, což zapisujeme jako PN(n). Počet podmnožin n (n₁, n₂, n₃, … n_k) je počet tříd, které značíme k. Platí, že počet tříd PN(n) = n. Proto se obecný počet tříd neuvádí. Třídu uvádíme pouze v případech, kdy potřebujeme pouze konkrétní jednu třídu. Potom zapisujeme PN(n,k). Například PN(4,2) = 3+1, 2+2. Druhá třída PN(4) sestává ze dvou řádků (lépe jednotlivých stavů rozdělení n). PN(n) samo o sobě nezná variaci pořadí, ale v rámci enumerací schemat kauzálních množin (a tedy také množin přirozených) pořadí hraje úlohu.

Postup rozvoje přirozené množiny – příklad k = 4 :

1. Máme 4 prvky v jedné podmnožině. Prvky mají vzájemný dotyk n₁ = 4. Třída 1.

2. Oddělíme 1 prvek od zbytku a získáme 2 podmnožiny n₁ = 3, n₂ = 1. Třída 2. Totéž můžeme udělat i opačně n₁ = 1, n₂ = 3. Třída zůstává.

3. Kauzálně máme 2 podmnožiny a všechny prvky můžeme vložit do n₂. Potom n₁ = 0 prvků, naopak n₂ = 4 prvky. Tím dokazujeme jen to, že n₁ má maximálně 4 prvky a n₂ také tak.

4. Stejným postupem můžeme vytvořit 3 podmnožiny. Získali jsme 3. třídu PN(4). Například 2+1+1, 1+2+1, 1+1+2 a podobně do n₃ vložíme všechny prvky. Takto dokážeme že i n₃ může mít maximálně 4 prvky.

5. Ze 4 prvků můžeme vytvořit maximálně 4 podmnožiny a dokázat, že každá z nich může mít maximálně 4 prvky. Získali jsme 4. třídu.

6. Kauzálně nemůžeme dokázat více podmnožin a ani větší mohutnost každé podmnožiny.

Tolik ke kauzálnímu dokazování, které říká, že pomocí k prvků můžeme dokázat maximálně n = k².

Neznamená to, že kauzální n musí být rovno k². Připouštíme n(k, k+1, … , k²). Z tohoto vyplývá relativnost kauzálních množin (n,k). Například k = 4, n = 12 nám říká že z počtu všech možných 12 kauzálních prvků můžeme vybrat některé 4 prvky. Taková množina je kauzální, ale není přirozená. Kauzální množina má nyní diskrétní n i k.

Intuitivně chápeme, že enumerace na kombinatorických množinách provádíme kombinacemi, nebo variacemi. Pro daný výpočet jsou (n, k) konstantní.

Představou přirozené množiny je čtvercová matice o stranách k. Vycházíme z toho, že čtverec dokazujeme jako 1. a poslední třídu PN(n). pro představu PN(4) :

1. třída 1. = (4)

2. třída 2. = (3+1)

3. třída 2. = (2+2)

4. třída 3. = (2+1+1)

5. třída 4. = (1+1+1+1)

Počet všech možných n přirozených množin je dán počtem podmnožin podle poslední třídy PN, zatímco počet prvků v podmnožině je dán 1. třídou PN. Čtverec chápeme jako grafickou reprezentaci, zatímco formu PN(n) jako numerickou.

Výpočty nad přirozenými množinami

Výše jsme si uvedli skutečnost, že pro pochopení podstaty přirozené množiny je potřebné chápat základ v PN. Pro výpočty (enumerace) nad přirozenými množinami to platí dvojnásob. Pro enumerace používáme jak kombinace, tak variace. To si musíme vysvětlit nejlépe na přirozené množině k = 7, která má n = 7² = 49. Je to shodou okolností podoba s modelem loterie 6+1/49. Přizpůsobíme si „loterii 6/49“ na „loterii 7/49“ aby model odpovídal přirozené množině.

Ze zadání vyplývá, že jde o čtverec 7*7 který reprezentuje 7 řádků po sedmi číslech. Do tohoto čtverce může být náhodně uspořádáno (vylosováno) 7 prvků. Podle PN(7) existuje 15 různých možností uspořádání. Extrémní jsou 2 případy, konkrétně 1. a poslední (15.) řádek.

Váha výpočtu

1. buď 7 v některém jednom řádku. Počet možností (váha) 7 = C(1,7)

2. nebo 6+1 v některých dvou řádcích. Počet možností (váha) 7*6 = 42 = V(2,7)

3. nebo 5+2 v některých dvou řádcích. Počet možností (váha) 7*6 = 42 = V(2,7)

4. nebo 5+1+1 v některých třech řádcích. Počet možností (váha) 7*15 = 105 = C(1,7)*C(2,6)

5. nebo 4+3 v některých dvou řádcích. Počet možností (váha) 7*6 = 42 = V(2,7)

6. nebo 4+2+1 v některých třech řádcích. Počet možností 7*6*5 = 210 = V(3,7)

7. nebo 4+1+1+1 v některých 4 řádcích. Počet možností (váha) 7*20 = 140 = C(1,7)*C(3,6)

8. nebo 3+3+1 v některých 3 řádcích. Počet možností (váha) 21*5 = 105 = C(2,7)*C(1,5)

9. nebo 3+2+2 v některých 3 řádcích. Počet možností (váha) 7*15 = 105 = C(1,7)*C(2,6)

10. nebo 3+2+1+1 v některých 4 řádcích. Možnosti (váha) 42*10 = 420 = V(2,7)*C(2,5)

11. nebo 3+1+1+1+1 v některých 5 řádcích. Možnosti (váha) 7*15 = 105 = C(1,7)*C(4,6)

12. nebo 2+2+2+1 v některých 4 řádcích. Možnosti (váha) 35*4 = 140 = C(3,7)*C(1,4)

13. nebo 2+2+1+1+1 v některých 5 řádcích. Možnosti (váha) 21*10 = 210 = C(2,7)*C(3,5)

14. nebo 2+1+1+1+1+1 v některých 6 řádcích. Možnosti (váha) 7*6 = 42 = C(1,7)*C(5,6)

15. a nebo 1+1+1+1+1+1+1 v každém řádku jednička. Váha = 1

Váha výpočtu je zásadní záležitost. Velmi výrazně usnadňuje enumeraci. Slouží také k pochopení výpočtů nad kauzálními množinami, které mají dvě a někdy i více stejných podmnožin n.

Váha patří mezi variace, respektive permutace. Přes to ji lze vyjádřit pouze kombinacemi. Vzorce mají většinou více ekvivalentních možností. To si musíme vysvětlit. Například :

13. řádek 2+2+1+1+1 v některých 5 řádcích. Možnosti (váha) 21*10 = 210 = C(2,7)*C(3,5).

Váhu zde uvádíme v jediném případě jako součin kombinací C(2,7)*C(3,5). Při tom vycházíme ze schematu, 2+2+1+1+1, který by měl správně vypadat takto 2+2+1+1+1+0+0. Vidíme dvě dvojky, tři jedničky a dvě nuly. Schema si můžeme představit v různém uspořádání a použijeme raději písmena místo číselných značek A = 2, B = 1, C = 0, :

• (2+2) + (1+1+1+0+0) = (A+A) + (B+B+B+C+C), proto A obsahují dvě podmnožiny ze sedmi, a to zjistíme jako C(2,7) zbylých 5 podmnožin obsahuje dva druhy prvků, proto pokračujeme (B+B+B)+(C+C). B je obsaženo ve třech podmnožinách z pěti proto použijeme vzorec C(3,5). Ve výsledku tedy C(2,7)*C(3,5) = 210

• Postup výpočtu můžeme modifikovat (C+C) + (A+A+B+B+B), proto C obsahují dvě podmnožiny ze sedmi, a to zjistíme jako C(2,7). Nyní bychom měli vyjádřit počet variant pro uspořádání A ve zbylých 5 podmnožinách, tedy C(2,5). Výsledek C(2,7)*C(2,5) = 210. Vidíme, že oba výpočty mají stejný výsledek C(2,7)*C(3,5) = C(2,7)*C(2,5). To není nic záhadného pokud známe vlastnosti řádku Pascalova trojúhelníku kde existuje souměrnost podle středové osy. Například C(0,7) = 1 = C(7,7), nebo C(1,7) = 7 = C(6,7), a tak dál.

• Další podobnou modifikací může být (B+B+B) + (A+A+C+C). Zde bychom postupovali buď C(3,7) * C(2,4), nebo ekvivalentně C(4,7) * C(2,4), protože C(3,7) = C(4,7). Výsledek je vždy stejný 210.

Při stanovení algoritmu můžeme vycházet nejlépe z uspořádání na schematu, což vyhovuje celkem dobře při zpracování váhy manuálně (výpočtem v hlavě, nebo záznamem vzorců do sešitu). Musíme si ukázat ještě jiné možnosti například řádek číslo 6 (4+2+1) :

Schema 4+2+1 musíme upravit na 4+2+1+0+0+0+0. Opět provedeme substituci za písmena, tedy A+B+C+D+D+D+D. Ve výpočtu nahoře je uvedeno V(3,7), tedy 7*6*5 = 210. Toto může modifikovat například na C(4,7) * 3!, tedy 35*6. Nyní jsme upřednostnili počet znaků D, což jsou nuly. Zbytek už je jen faktoriálem čísla 3.

Dostáváme se k tomu, že postupů může být vícero správných, ale musíme zvolit takový který má pokud možno jednotný a snadný algoritmus. Takovým postupem je uspořádání podle počtu opakování stejných značek a nejlépe sestupným řazením tak jak je tomu právě u PN.

PN je unární množina, která nezná nulu, ale substitucí za značky to vyřešíme uspokojivě. V mnoha případech je prázdná podmnožina nejpočetnějším druhem a i pro stroj snadnější postup vyžádá přípravné uspořádání. Pro představu PN(100) 50+40+10, Tedy A = 50, B = 40, C = 10, D = 0. Uspořádáme 97D, 1A, 1B, 1C (bez značek 97,1,1,1). Tedy C(97,100) = C(3,100) * 3! = 161700 * 6 = 970200, ačkoliv V(97,100) ještě není na hranici strojního zaokrouhlování a je to dobře spočetné.

Jenomže i variace, nebo faktoriál lze řešit pomocí kombinací. Potom algoritmus výpočtu vypadá takto : C(100-3, 100) * C(1,3) * C(1,2), respektive C(100-3, 100) * C(1,100-97)*C(1,100-98).

Musíme vědět, že faktoriál je možné vyjádřit součinem kombinací. Pro 7! takto :

C(1,7) * C(1,6) * C(1,5) * C(1,4) * C(1,3) * C(1,2) * C(1,1). Pro vlastní faktoriál to nemá valný význam, ale pro variace už uplatnění nalezneme zejména v cyklech, kde dekrementujeme n podle k.

Celkový výpočet (váha * základní výpočet)

1. 7+0+0+0+0+0+0 váha 7*C(7,7) = 7

2. 6+1+0+0+0+0+0 váha 42*C(6,7)*C(1,7) = 2058

3. 5+2+0+0+0+0+0 váha 42*C(5,7)*C(2,7) = 18522

4. 5+1+1+0+0+0+0 váha 105*C(5,7)*C(1,7)*C(1,7) = 108045

5. 4+3+0+0+0+0+0 váha 42*C(4,7)*C(3,7) = 51450

6. 4+2+1+0+0+0+0 váha 210*C(4,7)*C(2,7)*C(1,7) = 1080450

7. 4+1+1+1+0+0+0 váha 140*C(4,7)*C(1,7)*C(1,7)*C(1,7) = 1680700

8. 3+3+1+0+0+0+0 váha 105*C(3,7)*C(3,7)*C(1,7) = 900375

9. 3+2+2+0+0+0+0 váha 105*C(3,7)*C(2,7)*C(2,7) = 1620675

10. 3+2+1+1+0+0+0 váha 420*C(3,7)*C(2,7)*C(1,7)*C(1,7) = 15126300

11. 3+1+1+1+1+0+0 váha 105*C(3,7)*C(1,7)*C(1,7)*C(1,7)*C(1,7) = 8823675

12. 2+2+2+1+0+0+0 váha 140*C(2,7)*C(2,7)*C(2,7)*C(1,7) = 9075780

13. 2+2+1+1+1+0+0 váha 210*C(2,7)*C(2,7)*C(1,7)*C(1,7)*C(1,7) = 31765230

14. 2+1+1+1+1+1+0 váha 42*C(2,7)*C(1,7)*C(1,7)*C(1,7)*C(1,7)*C(1,7) = 14823774

15. 1+1+1+1+1+1+1 váha 1*C(1,7)*C(1,7)*C(1,7)*C(1,7)*C(1,7)*C(1,7)*C(1,7) = 823543

Ukázková tabulka výpočtu modelu loterie 7/49

Význam výpočtů nad přirozenými množinami

Výpočty tohoto typu jsou formou „Rozšířeného hypergeometrického rozdělení jevu pravděpodobnosti“. Správně provedený výpočet je dán vždy jako kombinace celkového n a k. Proto platí, že výpočet nad n-ticemi musí v součtu za řádky dát C(k,n) pro každý případ rozdělení na n-tice. Tím je potenciálně jakékoliv rozdělení podle PN(n). Například PN(49) má 173525 různých řádků. Každý s těchto řádků je možné považovat za systém n-tic, které můžeme (musíme) enumerovat pomocí PN(k) vždy se stejným výsledkem. Bez PN se neobejdeme a totéž platí pro váhu výpočtu. Prakticky se jedná o výpočty nad velice různorodými schematy.

Původní Hypergeometrické rozdělení umí pracovat pouze se dvěma díly n (n-ticemi). Výpočty nad n složeného z více dílů (n-tic) nebyly nikdy publikovány. Nepochybuji o tom, že pokusy provedení takových výpočtů nad více n-ticemi byly prováděny, ale zřejmě bez úspěchu. Problémem je zřejmě „váha výpočtu“, kterou je nutné pochopit jako obecnou permutaci, která se projevuje různě.

Jde o to, zda v systému n existují dvě, nebo více stejných podmnožin. Právě postup výpočtu nad stejnými podmnožinami n nám demonstruje výpočet nad přirozenou množinou.

Pokud systém n-tic neobsahuje dvě (nebo více) stejných dílů n, je váha výpočtu rovná jedné, ale podléhá variaci i v případě, že existují dvě, nebo více stejných k-tic. Někdy se stane, že váha dvou řádků (nebo více) je stejná, ale způsobená jiným uspořádáním v n-ticích. Takové případy sice akceptujeme v souhrnech, ale výpočet řádku zobecňovat nemůžeme.

Význam pro kombinatorické pojmy „s opakováním“

Jedná se o princip variací, kombinací a permutací „s opakováním“. Jsou to z logického hlediska na základě lingvistického významu nesmysly a tyto musíme chápat jako „nekauzální“, respektive jako kauzální nepřímo (nepřímá kauzalita).

Příklad 7⁷ je typicky případem variace s opakováním. Podle současné a konkrétní interpretace jde o n^k = nⁿ. Podle všeho n = 7 a potenciálně k(0, 1, … , n, … , ∞). Tento případ najdeme jako 15. řádek výše uvedeného výpočtu.

15. řádek 1+1+1+1+1+1+1 váha 1*C(1,7)*C(1,7)*C(1,7)*C(1,7)*C(1,7)*C(1,7)*C(1,7) = 823543. Váhou je jednička (můžeme ji zanedbat) a základní výpočet = C(1,7)⁷ = 7⁷. Z toho je zřejmé, že vzorec variací s opakováním je mocninou kombinací první třídy dílu n (n-tice).

Když budeme vycházet z Pascalova trojúhelníku (PT), tak můžeme vzorec kombinací zaměnit s jeho výsledkem, neboli koeficientem a dostáváme právě klasický pojem s opakováním. Nejde tedy přímo o chybu, jen o interpretaci, respektive lingvistický význam. Žádný prvek se neopakuje, ale zavedená konvence pojmu akceptuje zjednodušený výraz ve vzorci. Proto o výrazech s opakováním budeme hovořit jen jako o kauzálních nepřímo, respektive nekauzálních. Je to kompromis, ale současně si nedokážu představit vhodnější výraz pro pojmy s opakováním.

Skutečností je, že vzorce, nebo jejich výsledek (koeficient) jsou ve skutečnosti podmnožiny. Tyto jsou navzájem podmíněné (jako jev pravděpodobnosti jsou vyloučené na některou jednici z počtu prvků v n-tici), ale jsou také svázané počtem n-tic. Celkové n daného systému je dáno součtem n-tic. Proto u variací s opakováním zjistíme celkové n z výrazu n^k jako n*k.

Příklad 6 hracích kostek vytváří dojem 6⁶, ale ve skutečnosti C(1,6)⁶. Podle pravidla n*k, dostaneme výraz C(1,6)⁶ => k = 6, n = 36 a také C(1,6)⁶ ⊂ C(6,36). Tento vztah můžeme popsat jako poslední 11. řádek rozvoje PN(6) a jeho velikost C(1,6)⁶ ⊂ C(6,6²), formou absolutního množství 46656 ⊂ 1947792, respektive 2,395 % z celku 1947792.

Význam pro oblast kombinatorických množin

Vzhledem k tomu, že doporučuji akceptovat původní pojmy s opakováním, je také potřebné upravit pojem prvků. Pro množiny s opakováním zavedeme unikátní „vícečlenné prvky“ (jako náhradu za podmnožiny). Toto je také následkem obvyklého výrazu „binární množiny“. Máme – li například 2⁴, je správně n = 8 (2*4). To vytváří obecnou (nematematickou) asociaci jako C(1,4)+C(1,4), názorně (1,1,1,1)+(0,0,0,0). Vzájemné vyloučení mezi podmnožinami znamená například :

(1¹,1¹,1⁰,1⁰)+(0⁰,0⁰,0¹,0¹), nebo třeba (1¹,1⁰,1¹,1⁰)+(0⁰,0¹,0⁰,0¹) …

Pochopení je snadnější pokud místo pojmu „binární množiny“ zavedeme jiný pojem konkrétně „množin s binárními prvky“. Takové prvky potom zaznamenáme jako p^1,0. Zápis odpovídá mnohem více vzorci variací s opakováním. Například tedy n(p₁¹,p₂⁰,p₃¹,p₄⁰). Σp^1,0 = 4. Nic takového jako množiny vícečlenných prvků v rámci teorie množin nelze připustit, ale například pro polynomy je to zavedená praktika. Nehovoří se sice o prvcích, ale o členech polynomu, které mají jen výjimečně velikost 1 (z nulové hodnoty). Proto je celkem logické hovořit pouze o množinách s binárními prvky, nebo například množinách s heximálními prvky (hrací kostky). Opět je to kompromis mezi kauzální skutečností a zavedenou praxí. Takže pojem množin s binárními (či většími) prvky je záležitost která se vztahuje pouze ke kombinatorice. Tyto pojmy mají automaticky nekauzální podstatu, což neznamená, že by tato podstata vedla k chybě. Dáváme tak najevo pouze to, že kauzalita je „skrytá“ v kombinacích a to nejen jako poslední třída rozvojů přirozených množin, ale také jako členy řádku Pascalova trojúhelníku – posloupností 2ⁿ.

Význam pro kombinatorické pojmy „bez opakování“

Jedná se vlastně o faktoriál, který akceptuje postupné vyloučení „použitého prvku“. Například faktoriál čísla 4 (4!) se nám vybaví jako součin 4*3*2*1, nebo 1*2*3*4.

Ve skutečnosti C(1,4)*C(1,3)*C(1,2)*C(1,1), tedy C(1,4-0)*C(1,4-1)*C(1,4-2)*C(1,4-3). Podobně chápeme variace bez opakování. Například V(2,4) = C(1,4)*C(1,4-1) a tak dál.

Celkem důležitá je podobnost zápisů vzorcem kombinací mezi variacemi bez opakování a naopak s opakováním například :

Variace bez opakování V(3,4) = C(1,4)*C(1,4-1)*C(1,4-2), respektive 3!C(3,4)

Variace s opakováním V’(3,4) = C(1,4)*C(1,4)*C(1,4), respektive C(1,4)³

Význam výpočtů nad kauzálními množinami

Původní význam výpočtu nad přirozenými množinami, kde se projevuje variace jako váha výpočtu platí v širším měřítku také pro výpočet nad množinami obecně, tedy pro C(k,n) kde k ≤ n. Stejně tak pro množiny, kde je sice n = k², ale kde počet n-tic ≠ k, nebo jsou n-tice různě mohutné.

Pro představu n = k² = 49(n₁ = 21, n₂ = 19, n₃ = 14, n₄ = 5). Systém n je sice druhou mocninou k, ale rozdělení je pouze do 4 podmnožin (n-tic) a každá je jinak mohutná. Výpočtové schema má jedinou váhu v každém řádku (1). Enumerace pomocí PN(7) platí v omezeném rozsahu podle omezení třídou. Schema obsahuje pouze 4 podmnožiny a tím jsou omezeny třídy PN(7). Tedy takto :

1. třída 7,

2. třída 6+1, 5+2, 4+3,

3. třída 5+1+1, 4+2+1, 3+3+1, 3+2+2

4. třída 4+1+1+1, 3+2+1+1, 2+2+2+1

Třídy 5. až 7 jsou vyloučeny počtem podmnožin. Je zřejmé, že počet k-tic, nemůže být větší, nežli počet n-tic. Také platí pravidlo, že do n-tice nevejde větší k-tice. Takový stav je vyloučený velikostí n-tice. Například 2. třída, stav 6+1 :

1. C(6,21)*C(1,19)*C(0,14)*C(0,5) = 1031016, 2. C(1,21)*C(6,19)*C(0,14)*C(0,5) = 569772,

3. C(6,21)*C(0,19)*C(1,14)*C(0,5) = 759696, 4. C(1,21)*C(0,19)*C(6,14)*C(0,5) = 63063,

5. C(6,21)*C(0,19)*C(0,14)*C(1,5) = 271320, 6. C(1,21)*C(0,19)*C(0,14)*C(6,5) = Chyba.

Řádek 6 obsahuje k > n, tedy C(6,5) je chybou a tím je vyloučen celý 6. řádek (výpočet = 0). Takových řádků, které je nutno vyloučit bývá podle zadání často také poměrně mnoho.

Názorný příklad vyloučení počtem n-tic a velikostí n-tice ukazuje na složitou přípravu pro enumeraci která je ještě umocněna váhou v případě, že některé 2, nebo více n-tic jsou stejné. Váha se projeví jen v případech kdy do stejných n-tic náleží také stejné k-tice.

Význam přirozené množiny v teorii rozpisu

Teorie rozpisu je také novým pojmem, který má určitou obdobu v teorii grafů, nebo uspořádaných množin. Teorie rozpisu se zabývá vším co nazýváme například „řády“, tedy jízdní, pracovní nebo podobně „grafikony“, výrobní postupy, recepty, pravidla, nebo organizační uspořádání, popřípadě omezení, plán a v obecné úrovni algoritmy. Připomeneme jenom, že v rámci kombinatoriky odlišíme pojmy „výpis“, „etalon“ a „rozpis“. Konkrétně rozpis ⊂ výpisu a etalon je uspořádaný výpis (vzestupně, nebo sestupně jak v řádku, tak ve sloupci).

Pod pojmem rozpis se tradičně rozumí rozpis na sportovní, nebo hazardní hry. Ve sportovní terminologii je to zejména pyramida rozpisu turnajových utkání. Dobře známým prostředkem pro určení jednotlivých zápasů jsou „Bergrovy tabulky“, které se používají dodnes i když už existují jiné sofistikovanější prostředky.

Přirozená množina je v určitém smyslu také synonymem pro čtverec. Systémy čtverců mají celkem zajímavou vlastnost. Tato vlastnost je částečně známá jako „Latinské čtverce“, což je vlastnost typická pro čtverce sudých čísel, ale existují výjimky 2² a 4². Lépe na tom jsou čtverce lichých čísel, ale nejlépe na tom jsou čtverce prvočísel. Jde o obsah dvojic ve čtverci.

Obsah dvojic ve čtvercích

Analyticky se jedná o to, počet všech dvojic n = k² se dá uspořádat do k+1 čtverců. Ukázkově výpočet n = 9, k = 3 : Obsah dvojic z devíti C(2,9) = 36, trojice obsahuje C(2,3) = 3 dvojice, podíl 36/3 = 12 trojic, které obsahují všechny dvojice z celku 9. Výsledných 12 trojic lze uspořádat po třech tak, že vzniknou 4 čtverce 3×3 (3 řádky po 3 prvcích). Tedy 4 matice 3² = C(2,9).

Jiný příklad n=16, k=4 : Obsah dvojic ze šestnácti = C(2,16) = 120, čtveřice obsahuje C(2,4) = 6 dvojic, 120/6 = 20 řádků a 20/4 = 5 matic 4² = C(2,16).

Další příklad n=25, k=5 : Obsah dvojic ze 25 = C(2,25) = 300, pětice obsahuje C(2,5) = 10 dvojic, 300/10 = 30 řádků a 30/5 = 6 matic 5² = C(2,25).

Výše uvedené systémy včetně 2² lze kauzálně sestrojit jako rozpisy, ale u čtverce 6² (36) narazíme na bariéru známou jako problém „Latinských čtverců“. Zde sice platí výpočet, ale nelze sestrojit rozpis (maticovou grafickou reprezentaci) jako důkaz. Je to problém teorie čísel.

Podobná bariéra je i u dalších sudých čísel, ale víme že to neplatí pro čtverec čísla 2 a 4. Je tedy možné, že blok nemají ještě další sudá čísla. To bohužel nevím.

Také nevím zda lze dokázat, že systém lichých čísel blok nemá. Čím je liché číslo větší, tím je obtížnější vytvořit rozpis jako maticovou grafickou reprezentaci.

Naproti tomu vím, že u čtverců prvočísel žádný problém není. Existuje algoritmus, který bezpečně vede k vytvoření rozpisu (maticové grafické reprezentaci).

Proto je množiny n vhodné rozkládat do dvojic pomocí nejblíže vyšší čtverců prvočísel. V takovém případě nezáleží na tom, zda je číslo liché, nebo sudé.

Ukázky čtvercových matic

2² jako grafická reprezentace, analýza a výčet dvojic : C(2,4) = 6, C(2,2) = 1, celkem 6 řádků uspořádaných po dvou = 6/2 = 3 matice 2² podobně 3² a 4² :

Samozřejmě jde o souvislost nejen s geometrií, ale také s algebrou a filozofií, nebo s pojmovým vymezením.

Přirozená množina ve formě dvojic celku n reprezentuje formou grafické reprezentace jak plochu, tak prostor. Například pro analýzu platí, že každému k odpovídá přirozená množina k², a dvojice C(2,k²) mohou šetřit plošná i prostorová uspořádání, respektive neznámých v algebře.

Podobně můžeme k problému přistoupit jako k = sqrt(n) a to jak v množinách diskrétních, tak spojitých (kontinuálních). Pokud nám vyjde k různé od celočíselného násobku prvočísla, vytvoříme čtverec z nejblíže většího prvočísla a plníme od prvního řádku první matice. Dostaneme perfektní rozklady n-tic s obsahem všech dvojic, ačkoliv v různě mohutných k-ticích.

Uspořádání do prvočíselných matic je univerzálním prostředkem pro všechna k, respektive n mezi prvočísly. To opět vyžaduje názorný příklad :

Mějme n = 32. Potom k = sqrt(32) = 5,66. Nejblíže vyšším prvočíslem je 7. Proto řešíme schema jako C(2,49). Předem víme, že to bude 8 matic 7², tedy 56 řádků (8*7). Ve vytvořeném schematu buď zvýrazníme prvky 1 až 32, nebo smažeme prvky 33 až 49. M1 (první matice je souřadnicí), kterou nyní nepoužijeme. Také neuvádíme k jakému účelu je rozpis postaven. Mohou to být duely jednotlivců, nebo družstev. Rozhodčích uvádíme 21, z toho 7 hlavních (žlutě podbarveni). Předpokládejme, že se jedná o soutěž jednotlivců, a proto musí mít každá aréna minimálně 3 hrací plochy (tenisové kurty, stoly na šachovnice, nebo stolní tenis, žíněnky a podobně) :

Vlastní finále může mít rozličný počet finalistů. Každý den dá 14 potenciálních postupujících. Na konci každého dne se sečtou výsledky a určíme, že postupují dva hráči z celku 14 kandidátů. Za 7 dní to může být 14 hráčů, ale jeden, nebo jen dva dva hráči mohou být vítězi v každém dni. Proto vyjde nějaký počet finalistů, který se musí řešit jiným rozpisem. V semifinále se nemohou potkat hráči ze stejného sloupce. Například hráč číslo 1 se potká pouze 1x s hráči 8 až 32. S hráči 2 až 7 se potkat nemůže. Toto platí pro každého jednoho hráče. Schází totiž duely ze souřadnice. Hráči ale vystřídají všechny arény a většinu rozhodčích. Proto ve finále hraje každý s každým.

Každý den se v každé aréně potká 4, nebo 5 hráčů. Proto postačí 2 kurty (stoly apod.) na kterých hrají současně 4 hráči. Třetí „kurt, stůl, obecně hřiště“ slouží k tomu, aby se mohl začít zápas v případě že aréna vyžaduje úpravu povrchu, odstranění závady a podobně. Organizační (logistické) potřeby jsou 7 arén, každá se třemi „hřišti“ (21 hřišť) počtem 21 rozhodčích plus případně dojezdové doby a dopravní prostředky mezi „hřišti“.

Pokud bychom rozdělili 32 závodníků na poloviny, můžeme semifinále řešit dvěma systémy 4². V takovém případě bychom potřebovali pro semifinále 4 dny, 8 arén a celkem 24 hřišť, nebo také 24 rozhodčích. Jedinou výhodou je doba 4 dnů za kterou se odehraje semifinále.

Podobný je logistický problém městské, nebo příměstské dopravy. Zde bychom využili také souřadnici, proto 8 autobusů. Nyní bychom místo hráčů řešili zastávky. Například M2 až M8 pro rychlé otáčky při denních špičkách a souřadnici mimo špiček. U systému 2×4² by se daly propojit vždy 2 čtverce do jedné trasy a potom je vhodný počet autobusů 5.

Výhodou je nejen možnost použití všech dvojic ze systému, ale také optimální rozdělení na stejné, nebo hodně podobné díly.

Uspořádání dvojic v ploše a prostoru

Uváděli jsme si, že každá první matice k² je souřadnicí. Zbylé matice reprezentují vrstvy krychle s mohutností k³. Základ plošné grafické reprezentace spočívá v kombinacích, které řadíme zásadně vzestupně jak v řádku, tak ve sloupci. Pokud uvažujeme o použití pro prostorové uspořádání máme nejblíže k hlavolamu „Rubikova kostka“. Je zajímavé, že další podobnost můžeme hledat u objektů typu HyperCube, respektive teseraktů.

Rubikova kostka má nevýhodu. Tradiční kostka má pouze 26 (3³-1) krychliček protože uvnitř je kulový kloub, který drží pohyblivé segmenty. Využívá pouze 6 barev a tím se zdánlivě dá zamíchat libovolná kombinace. Není to pravda. Vrcholové segmenty budou vždy vrcholovými (3 barvy na 3 plochách) a podobně střední hranové segmenty (2 barvy na dvou plochách) i prostřední segmenty ploch, které mají pouze jedinou barvu na jedné ploše.

Existují různé druhy tohoto hlavolamu. Krychlové 2³, původní 3³, 4³, 5³ a libovolně větší včetně 6³, kde se vzhledem k principu nemůže projevit efekt „Latinských čtverců“. Existují také útvary čtyřstěnů (stejnostěnné pyramidy trojúhelníků), nebo dvanáctistěn (pětiúhelníkové stěny) a možná by šly podobně vytvořit také další Pytagorijské mnohostěny.

U teseraktů je tomu jinak. Zde existují i středové „krychle“. U rozpisů k³ platí podobná pravidla pro uspořádání elementů jako u manipulací s nadkrychlemi. Nejlepší představou je uspořádání podle hlavolamu „Sudoku“, které ale pro účely aplikací není podstatné.

Základem je změna pozic stěnových elementů celá stěna (zepředu – dozadu, z boku na opačný bok, shora – dolů), nebo naopak (zezadu – dopředu, z dola – nahoru ap). V každé prostorové ose mohou být 2 opačné směry. Celkem 6 různých směrů. Při těchto operacích dochází pouze k variaci a v žádné vrstvě se neobjeví některý prvek vícekrát.

Jiným případem je rotace stěny, která způsobí, že se objeví ve stěnách „opakování stejných prvků“. Toto můžeme pokládat za „chybu“, ale v praxi to můžeme využívat jako „šifrování“. Například krychle 3³ (27 elementů) může být spořádána až 27! krát jinak (1,09E+028). Správné uspořádání kombinací ve stylu Sudoku je 27 z tohoto počtu, tedy poměr 1 : 4,03291461126606E+026.

Toto je už velice zajímavé pro aplikace z oblasti kryptografie. Ale i vlastní kombinatorické vyjádření v plošných čtvercích může skrývat obsah v podobě souřadnice, kterou lze unikátně dopočítat, respektive v počtu řádků více nežli pouhou souřadnici.

K vyřešení (dopočítání) všech vazebních dvojic z k³ potřebujeme pouze (½ + 1) řádků ze všech řádků reprezentace. Například pro 2² (6 řádků) potřebujeme některé 4 řádky, pro 3³ (12 řádků) potřebujeme některých 7 z celku 12, pro 4³ (20 řádků) potřebujeme některých 11, pro 5³ potřebujeme některých 16 ze 30, pro 7³ potřebujeme některých 29 z 56, pro 9³ potřebujeme některých 46 z 90, pro 11³ potřebujeme některých 61 ze 121, s tak dál. Platí pravděpodobně pravidlo, které říká, že pro obsah dvojic je nutné získat ½ + 1 řádek, což garantuje invariantní dopočítání (rekonstrukci) celkového počtu řádků.

Na závěr zajímavosti

Teorie rozpisu souvisí úzce s přirozenou množinou. Jako zajímavost si uvedeme rozpisy na kurzové sázky a loterie, což jsou tradičně vhodné modely pro demonstraci.

Množiny dvojic (trojic a podobně) se dají zkonstruovat do formy rozpisu s obsahem všech dvojic, ale nejedná se pouze o symetrické čtverce. Ukážeme si rozpis všech dvojic z celku C(2,7) = 21 dvojic do sedmi trojic. Takových uspořádání je více, ale za všechny příklad :

Rozpis obsahuje všechny dvojice uspořádané do trojic. Ten obsah je garancí. Garantuje uhodnutí pokud je chybou jeden, nebo 2 tipy. Další výhry jsou již dány pravděpodobností (bez záruky).

Rozpis obsahuje 7 trojic z celku 35 = 20%. Při chybě 4 z celku 7 s pravděpodobností 20% uhodneme 1 tip a můžeme i maličko vydělat, pokud jsou součiny kurzů kurz³ > 7. Takový případ nastává při kurzech dvě a více. Například 2³ = 8 (zisk +1), 2,08³ = 9 (zisk +2), nebo při kurzu 2,2³ = 11 (zisk +4).

Pravděpodobnost při chybě 3 z celku 7 (4 tipy správně) je opačná 80%. Pokud se 3 chyby vyskytnou ve stejném řádku, neuhodneme žádný tip, jinak uhodneme 1 správně tipovanou trojici.

Při chybě 2 tipovaných zápasů máme garantovanou výhru dvou trojic. Je to logické, protože máme všechny dvojice a každé číslo se v rozpisu opakuje 3x. Jednou se chyba vyskytne ve dvojici stejného řádku, tedy 1 společný řádek (obsahuje obě chyby) + 2 krát 2 řádky s jedním chybným tipem = 5 chybných řádků z celku 7.

Při chybě 1 tipu uhodneme 4 trojice (protože se každé číslo a tedy i chyba opakuje 3x).

Samozřejmě pokud neuděláme žádnou chybu vyhrajeme 7 trojic. Souhrn vypadá následovně :

5 až 7 chyb ⇒ ztráta 7 sázek
4 chyby ⇒ ve 20% uhodnutí 1 tipu při kurzu 2 bilance ( -7, +8) = +1
3 chyby ⇒ v 80% uhodnutí 1 tipu při kurzu 2 bilance ( -7, +8) = +1
2 chyby ⇒ garance 100% uhodnutí 2 tipy bilance ( -7, +16) = +9
1 chyba ⇒ garance 100% uhodnutí 4 tipy bilance ( -7, +32) = +25
0 chyb ⇒ garance 100% uhodnutí 7 tipů bilance ( -7, +56) = +49

Takové opatrné sázení odporuje mentalitě hazardérů. Naopak se většina z nich holedbá, že uhodne téměř vždy 5 z celku 7 sázek zejména když si je vybírají sami. Dle mých zkušeností to není pravda protože i „sportovní odborníci“ se pohybují jen těsně nad hranicí průměru, což je 1/3 z celku 7 (tedy průměr 2,33), a i s výhodou znalostí průměrně uhodnou 3, nebo 4 příležitosti z celku 7. Avšak i toto může vést dočasně k pozitivní bilanci.

Celková pravděpodobnost vychází z předpokladu, že nejmenší kurzy > 2 (na tři druhy výsledků fotbal, hokej) mají pravděpodobnost 33% a rozdíl mezi kurzy jednotlivých výsledků jsou statisticky zanedbatelné. Celková pravděpodobnost se spočítá jako pravděpodobnost všech možných případů mezi extrémy kdy neuhodneme žádný tip, nebo naopak všechny :Tabulka ukazuje, že i při maximálně 4 chybách je sázející ve ztrátě. To se mění až v případě, že dokáže tipovat s maximálně třemi chybami ze sedmi :

Vidíme zcela zřetelně, že v případě maximálního počtu 3 chybně tipované je možné docílit průměrného zisku. Pozitivní bilance umožňuje ještě také nějaké chyby navíc. Takže můžeme vyjádřit skutečnost, že odborník může ze sázení profitovat až když tipuje správě a pravidelně nejméně 4 sázkové příležitosti z celku 7 možných. Pravděpodobně je zde souvislost mezi schopností rekonstrukce při zadání ½ + 1 řádek, tedy uhodnout ½ + 1 tip ze všech.

Avšak takto úspěšné tipování je fenomenální a spíš bych tipoval, že nejde o poctivou sázku. Pravidelně správně tipovat 57 %, nebo dokonce 71% (2 chyby) asi nelze ani v rámci omezených duelů národní ligy, ale snadno se stane, že po určitou dobu může sázející profitovat, i když si tento profit musíme přepočítat na investice a zvážit kolikrát za sebou se může opakovat neúspěch. Investicí je počet všech možných 116280 sázek proti zisku 12054 = cca 10%

Výpočet je proveden upraveným hypergeometrickým rozdělením pravděpodobnosti, což je asi neobvyklé (jde o klasický výpočet, ale bez relativní četnosti). Náhradní schema vychází z poměru n = 3 díly (1+2) a do každého dílu se vejdou všechny možnosti. Takže uhodnutí 1 díl = 7 a opakem jsou 2 díly = 14, tedy n₁ = 7, n₂ = 14, celkem n = 21 a k = 7.

Bilance vychází z toho, že je použit minimální kurz 2. Obvyklým postupem je násobení pravděpodobností, který ale není korektní. Z pohledu účetnictví by se měly započítat položky nákladů a od nich odečítat výtěžek. Místo toho jsme použili bilanční výsledek každého případu a vynásobili absolutní hodnotou četnosti. Tuto potom sčítáme.

Tou zajímavostí je právě ziskovost sázení za předpokladu, že sázející neudělá více, nežli 3 chyby.

Jak náš rozpis vznikl to si ukážeme opět na obrázku. Nejde o nic složitého. Ze symetrického sytému čtvercových matic vytvoříme systém větší pomocí postupu „Actus“ :Na obrázku vidíme znázornění jak ze symetrického systému matic vzniká systém nesymetrický přidáním číslic k původnímu systému. Tento princip platí jako rozvoj všech symetrických systémů. Například ze systému matic 3² C(2,9) = 4 matice 3×3 vznikne 13 řádků nesymetrického systému C(2;13), řádek 4 číslice, ze systému 4² tedy C(2,16) – 5 matic vznikne 21 řádků C(2,21) s řádkem 5 číslic a tak dál.

Jiný příklad loterie KENO 20 z 80. Tento příklad spadá pod čtverec devítky, ale jedno číslo musíme ignorovat (81). Přirozenou množinou tento systém není hned ze dvou důvodů. Jak uvádíme výše, počet n = 80 nemůže být úplným čtvercem, a k je mnohonásobně větší nežli sqrt(80). Přes to můžeme poznatky přirozené množiny úspěšně akceptovat zejména z pohledu výpočtu.

Nejprve ale trošku logického uvažování. Při losování 20 z celku 80 je losovaná úplná čtvrtina všech možných. Když si představíme neúplný čtverec devítky do kterého „vylosujeme“ 20 čísel dostaneme 2 extrémy :V nejlepším případě dostaneme dva plné řádky – dvakrát devítku. V nejhorším případě dostáváme ve dvou řádcích trojici. To znamená, že většina případů je někde mezi těmito extrémy. Pokud bychom vsadili všechna čísla do devíti řádků podle matice (s libovolným uspořádáním v řádcích), nemělo by se stát, že neuhodneme žádnou výhru. To záleží samozřejmě na tom, jak jsou výhry definovány v herním řádu. Připomeneme, že rozpis obsahuje 10 matic.

Základ této hry je používán ve vícero podobách. Původní model neobsahoval žádná prémiová čísla („královská“, „šťastná“ a podobně.). U nás v ČR byl a je doposud tento model provozován pod názvem „Šťastných 10“ i když se dost změnil – statistika je k dispozici pouze rok zpětně. Losuje se 2x za den, takže k dispozici je pouze 730 výsledků.

U původního modelu, který se používal bez „královského čísla“ za celou dobu losování vracel rozpis C(2,80) kolem 52% investic a překračoval nominální výhernost. Statistika byla vedena od úplného začátku a pokračovala ještě dlouho po zavedení „královského čísla“, ale to už je také historie.

Upozorňuji, že těch 52% vracel rozpis dlouhodobě a bez výrazného kolísání. Za současného stavu kdy jsou provozovány 2 různé hry je to podobné. I když každá z her má jiné parametry : Výhernost je 45,51 % u běžné (základní) hry, a 59,70 % u královské hry tedy průměrně obě hry dohromady 52,6%, což je důkaz toho, že rozpis funguje stejně dobře, ale i toho, že analytici umí dobře upravit výhernost modelu hry.

Jedná se o statistiku za 1 rok a dvě losování denně. Systém pevných výher je zdrojem určitého kolísání výhernosti, která je standardně nastavena na 50% vkladů. Zajímavé je, že základní hra vykazuje nejmenší výhru rozpisu 1 (kurzový bod) a při tom má více řádků s pozitivní bilancí nežli královská hra a při tom má menší celkovou výhernost. Královská hra má nejmenší výhru 20 kurzových bodů, ale pozitivní bilanci řádků (výsledek za řádek je ziskový) má menší, zato výrazně vyšší nežli běžná hra.

Tento rozpis obsahuje 10 matic. Každá matice obsahuje 8 řádků po devíti číslech a jeden řádek 8 čísel. Celkem tedy za 10 matic 80 řádků po devíti číslech a 10 řádků po osmi.

Co je na tom zajímavé? Rozpis vždy vyhraje nějakou výhru i když většinou malou. Přes to se chová v poměru stejně jako bychom použili plný výpis (devític). Výherní kvóta je stanovena na 50% vkladů. Je to efekt holografického střepu. Současné teorie pravděpodobnosti nic takového neuvádí a nezná princip který říká, že pravidelně rozložený systém rozpisu průměrně vrací poměr výherní kvóty. Výpočet pravděpodobnosti podle stávající teorie se vztahuje na poměr počtu všech vsazených k počtu možných a v případě loterií také podle rozložení výher.

Soubor s makry a rozpisem můžete stáhnout zde KENO 20_80, nebo zde KENO 20_80. Sešit je formátem ODF (LibreOffice). Makra budou fungovat pouze v LibreOffice a Apache OpenOffice. Sešit obsahuje 2 listy vyhodnocení, takže makra budete potřebovat jen pro ověření aktualizovaných výsledků stejné loterie, nebo přizpůsobení pro jinou loterii se stejným modelem hry.

Jev popsaný výše v konstrukci herního systému chybou není. Ten má dobře spočítané pevné výhry (vlastně kurzy) a lze ho modifikovat až téměř k úrovni „Rulety“. Bankéř u rulety profituje z jediného políčka. Model 20/80 by si mohl dovolit mnohem vyšší výhernost a přes to by si zisky udržel ačkoliv jde o loterii a nikoliv kurzovou sázku.

Příklad pro kurzové sázky. Uvedený systém teoreticky můžeme použít pro kurzové sázky, pokud lze nashromáždit dostatek vhodných sázkových příležitostí. Objasníme si, že pravděpodobnost kurzových sázek se řídí kurzem a typem sázky (například na tři výsledky, nebo na dva výsledky, na pořadí a ještě další druhy). Zjednodušíme skutečnost na tři druhy výsledků a pravděpodobnost 33% každého různého výsledku. Kurzové příležitosti jsou navzájem zcela nezávislé, což u loterií neplatí.

Pravděpodobnost nám roste v takovém případě lineárně, tedy vždy jde o třetinu. Přirozená množina jako n = k², respektive k = Sqrt(n) roste jinak, konkrétně s druhou odmocninou n. Při mohutnosti 9 prvků nastává rovnost 1/3 = sqrt(9) a při větším n je 1/3 větší nežli sqrt(n). Rozdíl mezi těmito parametry se dále zvětšuje.

Příklad n = 25, potom uhodnutí = 25/3 a tip sqrt(25), tedy uhodneme cca 8,33 tipů a rozpisem C(2,25) získáme 6 matic 5². Extrémy 1 uhodnutý tip 5 čísel a opačný extrém 3 tipy s uhodnutou dvojicí.

Příklad n = 49, potom uhodnutí = 49/3 a tip sqrt(49), tedy uhodneme cca 16,33 tipů a rozpisem C(2,49) získáme 8 matic 7². Extrémy 2 uhodnuté tipy 7 čísel a opačný extrém 2 tipy s uhodnutou trojicí.

Příklad n = 81, potom uhodnutí = 81/3 a tip sqrt(81), tedy uhodneme cca 27 tipů a rozpisem C(2,81) získáme 10 matic 9². Extrémy 3 uhodnuté tipy 9 čísel a opačný extrém 9 tipů s uhodnutou trojicí.

Příklad n = 121, potom uhodnutí = 121/3 a tip sqrt(121), tedy uhodneme cca 40,333 tipů a rozpisem C(2,121) získáme 12 matic 11². Extrémy 3 uhodnuté tipy 11 čísel a opačný extrém 7 tipů s uhodnutou čtveřicí.

Příklad n = 169, potom uhodnutí = 169/3 a tip sqrt(169), tedy uhodneme cca 56,333 tipů a rozpisem C(2,169) získáme 14 matic 13². Extrémy 4 uhodnuté tipy 13 čísel a opačný extrém 4 tipy s uhodnutou pěticí.

Příklad n = 289, potom uhodnutí = 289/3 a tip sqrt(289), tedy uhodneme cca 96,333 tipů a rozpisem C(2,289) získáme 18 matic 17². Extrémy 5 uhodnutých tipů 17 čísel a opačný extrém 7 tipů s uhodnutou šesticí.

Uvedenými příklady demonstrujeme rozdílnost růstu 1/3 z n proti sqrt(n). Nyní opět teoreticky uvedeme, že většina různých sázkových příležitostí se dá vyjádřit jako dva druhy výsledků. Například výsledky se třemi druhy se dají postavit jako tip základní proti dvojtipu. U sázek složených z mnoha příležitostí přestává hrát dominantní úlohu výše kurzu. Dvojtip má sice malý kurz, ale velkou pravděpodobnost (cca 2/3). Ale postačí nám pro úvahu jen 50%. Je zřejmé, že extrémy se s rostoucím n navzájem blíží – k 1/2.

Potom například n = 121, k = 11 s obsahem 132 řádků (tipů) a k dosažení zisku při výhře 1 tipu potřebujeme průměrný kurz 1,559 a více. Další příklad n = 169, k = 13 obsahuje 182 řádků (tipů). K docílení zisku při výhře 1 tipu potřebujeme průměrný kurz 1,49 a více. Pro n = 289, k = 17 s obsahem 306 řádků postačuje průměrný kurz 1,4 a více. Pozorujeme jak klesá potřebný kurz a naproti tomu se zvedají objemy extrémů jen na základě růstu množství n příležitostí.

Některé kurzové sázky složené z více příležitostí vyplácí výhry i v případě, že je jeden, nebo několik málo tipů v sázce chybných.

Jako reálná možnost vzhledem k počtu nabídek se jeví použití n = 49, k = 7 s obsahem 56 řádků (tipů) a k dosažení zisku při výhře 1 tipu potřebujeme průměrný kurz 1,777 a více, nebo i actus 57 řádků pro n = 57, řádek 8 sázkových příležitostí s minimálním průměrným kurzem 1,567. Lze tak vybírat kurzy kolem 2 celé a kombinovat s dvojitipy.

Jiný příklad – SUDOKU. Pro konstrukci Sudoku můžeme využívat systém C(2,9), který obsahuje 4 matice 3², z nichž je jedna pro Sudoku nevhodná (souřadnice).

Vypadá to sice na první pohled jako celkem nezajímavá metoda konstrukce rébusu. Podobných a pravděpodobně snadnějších je známo mnoho. Jenomže tato konstrukce umožňuje zakódovat všechny dvojice z celku 9 například dopočítávat „souřadnici“ jako tajenku. Je to posunutí Sudoku na vyšší úroveň. K dopočítání „tajenky“ je nutno znát 7 trojic z celku 12. Sudoku je systém C(2,9) bez souřadnice (ta je tajenkou) proto potřebujeme vyřešit v jednom sloupci 7 trojic z devíti.Z takové konstrukce následně odebereme čísla tak, aby byl rébus obtížně řešitelný. Složitost klasického řešení může být zvýšena nutností dopočítat dvojice také mimo souřadnici. Nakonec můžeme zvolit slovní výraz (9 znaků) a ten zaměnit za čísla pomocí substituce. Alfabetický výraz by neměl obsahovat redundanci znaků, ale i to lze někdy připustit.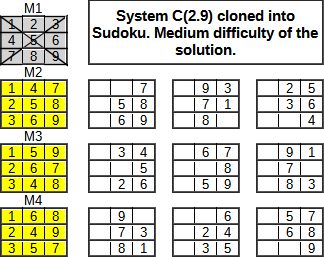Obrázek ukazuje upravený rébus tak aby obsahoval přiměřenou obtížnost řešení. Na příkladu vidíme 3x modifikovaný stejný systém C(2,9), což je opět běžná praxe. Existuje také zadání ze tří různých systémů kde se žádná trojice po uspořádání (velikost číslic zleva doprava vzestupně) neopakuje.

Je to sice hříčka pro zábavu, ale může to být použito například jako zdroj kódu pro zadávání hesla. Klávesnice 3×3 je celkem běžná. Často je nespolehlivá právě proto, že se vyťukává jen určitý počet znaků, což během času poznamená klávesy. Změnou na princip „Sudoku“ budou všechny klávesy používané stejnou měrou a pomocí systému C(2,9) je možné heslo měnit.

Není bez zajímavosti skutečnost, že všechny trojice z celku 9 se vejdou do sedmi systémů C(2,9), což vybízí měnit heslo pro každý den v týdnu, nebo hodinu v týdnu (168 hodin v týdnu znamená, že každá hodina v týdnu může podléhat modulo 7). Takových systémů trojic C(3,9) lze sestrojit 15360 různých, proto může být systematika využívána průmyslově například pro trezorové skříně s napojením na automatickou změnu hesla podle času, nebo s případnými kontrolními sekvencemi.