Kombinace vyjadřují počet všech unikátních k – členných uspořádání prvků z počtu n všech prvků možných. Fakticky k vyjadřuje počet prvků v řádku. Výpočet kombinací pak reprezentuje počet všech různých řádků (k-tic). Proto z pohledu výpočtu nahlížíme na jednotlivý řádek jako na prvek množiny kombinací.

Pojem kombinací bývá definován jako množina, kde nezáleží na pořadí prvků. To je ale poměrně dost zavádějící. Vystihuje to jen jakousi selskou vychytralost. Ta vychází z toho, že prvky mohou být mimo jiné (není to podmíněno) vybaveny například znakem čísla. Čísla mohou být přeházené v pořadí na řádku. – Stejně je čteme jako setříděné. Je to běžná praxe například při losování KENO a podobně.

Ve skutečnosti jsou kombinace podmnožinou variací. Kombinace od variací odlišíme jedině tak, že kombinace jsou setříděny v řádku vzestupně. Variace jsou typické tím, že nemají setříděné pořadí. Pravdou také je, že jsou nadmnožinou pro kombinace, a proto je také obsahují.

A ještě musím upozornit na jeden detail: Jsou – li kombinace definovány jako množina, nemohou mít „opakující se prvky“ – to lze zjistit nahlédnutím do každé poučky, která se zabývá množinami.

Kombinace se často používají jako nesprávný výraz. Lidově se používají často pro pojmy, které jsou ve skutečnosti například variacemi, nebo variacemi s opakováním.

Kombinace se zapisují nejčastěji takto A:
Tento vzorec se používá jako schematický zápis (konvence) pro tištěné odborné a školské publikace
Setkáme se také s následující podobou B:
Tento vzorec se používá nejčastěji jako zjednodušený zápis například ve skriptech, nebo jiných textech podobného účelu.
Nebo se setkáme také s následující podobou C: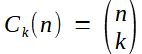Tento vzorec se používá podobně jako popis předchozí. Důvodem je pravděpodobně skutečnost, že textové editory neumí horní a dolní index zarovnat pod sebe.

Tvar vhodný pro zápis algoritmu D :Tento zápis využívá prakticky pouze faktoriál. Některé programovací jazyky mají takovou funkci předdefinovanou podobně jako tabulkové procesory a vzorec přímo vybízí ke snadnému přepsání do kódu.

Také se setkáme se syntaxí tabulkových procesorů D :
Combin(n;k)
To vychází ze syntaxe tabulkových procesorů, kde se takto zadávají parametry funkce „=COMBIN(n;k)“. Zápis pro účely schematického popisu (výrazová zkratka) může být v rámci této práce upraven například na „C(n.k)“. Setkáme se také s výrazem „C(k,n)“. Toto se také vyskytuje v odborných textech a původ je zřejmě v lingvistice. Lépe se vyjádří slovy „kombinace k-té třídy z celku n„, nežli „kombinace z celku n při výběru k„. V každém případě se používá libovolné pořadí pro n i k. Výjimkou je jenom binomický vzorec, kde jsou umístění standardně dané. Tuto variantnost připouštíme zejména proto, že konvencí je pevně dáno co je n i co je k.

____________________________________________________

Ještě musíme upozornit na zajímavou vlastnost, která říká, že výběrů k je stejně jako výběrů n – k. V Teorii kombinatoriky tuto vlastnost nazývám pojmem z algebry sigma – aditivitou. Správně je to „Partition Numerorum 2. třídy ze základu n„. Snadno to lze pochopit také nahlédnutím do Pascalova trojúhelníku. Například PN(9,2) – čteme : Partition Numerorum 2. třídy (k = 2) ze základu n = 9 .
0+9 = 9 → C(0,9) = C(9,9) ( = 1)
1+8 = 9 → C(1,9) = C(8,9) ( = 9)
2+7 = 9 → C(2,9) = C(7,9) ( = 36)
3+6 = 9 → C(3,9) = C(6,9) ( = 84)
4+5 = 9 → C(4,9) = C(5,9) ( = 126)
_____________________________
5 řádků představuje PN(9,2). Za šipkou doprava je obsah PT podle osy souměrnosti. Sečteme všechny různé kombinace : C(0,9) + C(1,9) + C(2,9) + C(3,9) + C(4,9) + C(5,9) + C(6,9) + C(7,9) + C(8,9) + C(9,9) = 512 = 2^9. Výraz 2^9 reprezentuje jednu celou Pascalovu třídu n což je vlastně celý 1 řádek v Pascalově trojúhelníku (PT). To má poměrně veliký význam – více v Teorii pravděpodobnosti.
_____________________________

Více je téma rozvedeno v RUBRICE Klasická kombinatorika
rubrika Algoritmy, kde je zveřejněno mnoho různých algoritmů, scriptů, maker a odkazů. V současné době (r 2022) existuje také vysvětlení v části „Nová kombinatorike“.