VÝZNAM DVOJIC PRO KONSTRUKTIVNÍ KOMBINATORIKU

Všechny množiny prvků z oboru čísel „N“ (celých kladných čísel) počínaje číslem dvě tvoří dvojice jednic. Proto lze každé číslo větší nežli 2 rozložit na dvojice. Některé výhody při takových operacích jsme si ukázali právě na pojmu Berger‘s Table. Na uvedeném příkladu jsme si ukázali také vytvoření trojic z celku všech dvojic.

Je to otázka – lze všechny trojice z celku 11 uspořádat stejným způsobem jak bylo ukázáno pro liché BT(11)? A když by to šlo, tak jak sestrojit plný systém všech trojic z celku 11?

Pokud lze vytvářet z dvojic trojice je také možné vytvářet k – tice vyššího řádu?

---

Na takové otázky existuje jednoznačně kladná odpověď. Ano lze konstruovat také vyšší třídy k – tic.

Nejprve si ale musíme vysvětlit co to jsou ty k – tice. Existuje ještě podobný výraz v podobě n – tice.

V běžné praxi se můžeme setkat s oběma výrazy, ale prakticky vždy znamenají totéž. Konkrétně se bude jednat o [u] nějakou podmnožinu.[/u]

Pojmy jsou důležité. Zejména jsou důležité pro kombinatoriku která by měla být jednoznačná. Budeme vycházet ze základního značení, třída (k) určitého celku (n). Běžně se setkáme například s výrazy „kombinace (k)-té třídy z celku všech možných (n)“. Podobně variace bez opakování, nebo i s opakováním. Už méně často (respektive vůbec) se nesetkáme s výrazem „Partitio Numerorum (k)-té třídy z celku (n)“. To je dáno zejména tím, že „Partitio Numerorum“ se označuje místo PN(n) značkou p(n) protože se uvádí pouze názvem „partition“ – to je velice zavádějící. Značku malé p, nebo velké P používá velmi mnoho oborů s různými významy. Nejbolestivější je právě souběh oblast matematiky a informatiky. Jeden z autorů ze začátku 20. století uváděl své vlastní pojmy pro oblast PN které se ale neujaly.

Na výrazy (n, k) je nutné nahlížet z pohledu množin dvěma různými způsoby. V drtivé většině případů převažuje názor, že (k) je podmnožinou z celku všech možných (n). Toto není vždy relevantní definice.

V rámci této práce se setkáme často s výrazy typu C(n.k), nebo také C(n,k,r). Výraz C většinou bude zaznamenat skutečně kombinace, ale je to obecnější pojem. Klidně si pod tím představíme jakýkoliv kombinatorický výraz. Tedy kombinace, Variace s (i bez) opakování, PN, nebo i faktoriál. To C si popíšeme jako obecný COMPUTING, nebo také COUNTING FOR COMBINATORICS.

DEFINICE MNOŽINY, PODMNOŽINY V KOMBINATORICE.

Když je (k) podmnožinou (n) jak se může stát že také podmnožinou není. A jak se to pozná?

Toto je zřejmě jedno s dilemat kombinatoriky. Názorně si to uvedeme jako loterii RULETA, nebo model loterie 6/49. Představíme si klasickou ruletu – tedy rotující (nebo i zastavené) kolo se všemi čísly. Podobně model 6/49 (ať už se losuje jakýmkoliv způsobem).

Dejme tomu že se kolo, nebo buben točí ale ještě nejsou vylosovány žádná čísla. Klasická francouzská ruleta obsahuje 37 čísel. Nežli se vhodí kulička, ale ještě i poté co se vhodí a není usazena – není množina (k) podmnožinou (n). Existují dvě nezávislé množiny konkrétně n(37p)[p1^0, p2^0,……p37^0] a k[1p^1]. Teprve po sjednocení vzniká systém kombinací 1. třídy celku 37. Tedy zápis notací tabulkových procesorů COMBIN(37,1).

Podmnožinou se podobně stane model loterie 6/49 až když se vylosuje všech 6 prvků základního modelu. Při tom dochází ještě k dezinformaci. Losují se variace, ale vyhodnocují se jako kombinace. Jedná se o postupné navyšování systému v tomto smyslu :

1. Combin(49;0) = 49p^0 před vylosování prvního čísla
2. Combin(49;1) = 48p^0 + 1p^1 po prvním vylosovaném
3. Combin(49;2) = 47p^0 + 2p^1 po druhém vylosovaném
4. Combin(49;3) = 46p^0 + 3p^1 po třetím vylosovaném
5. Combin(49;4) = 45p^0 + 4p^1 po čtvrtém vylosovaném
6. Combin(49;5) = 44p^0 + 5p^1 po pátem vylosovaném
7. Combin(49;6) = 43p^0 + 6p^1 po šestém vylosovaném

Jde skutečně o variace které se počítají jako součin 49*48*47*46*45*44*43. Rozdíl v podobě podílu mezi počtem variací a kombinací stejné třídy a stejného základu je dán počtem 6! (faktoriál čísla 6 který je roven číslu 720).

Konkrétně Variace(49;6) = 6!*Kombinace(49;6). Aby to bylo zřetelnější otočím vztah Kombinace(49;6) = Variace(49;6)/6!

Aby byl model her typu 6/49 skutečně modelem kombinací, musely by se prvky (kuličky ap.) losovat naráz a nikoliv postupně. Lepší by byla představa rulety se 49-ti čísly a naráz by se vhodilo 6 kuliček. Konec losování by nastal až po usazení všech kuliček.

U popisu herního modelu 6/49 jsme si popsali co to jsou k – tice. Obecně to jsou podmnožiny z celku (k)

Ruleta nám naproti tomu ukáže n – tice. Dá se sázet na díly – například sudá – lichá, na třetiny a podobně. Jsou to tedy podmnožiny z celku (n).

---

Nejde ale o loterie nebo způsoby losování. Nemělo by být zejména pro odborníky překvapením, že rozhodující je ČAS.

MATEMATICKÝ ČAS A DVOJICE SYSTÉMU

Nejprve se vrátíme zpět ke dvojicím a pak si podáme důkaz o MATEMATICKÉM ČASU. Ukázali jsme si dvojice ve formě rozdělené do BT. Systém je kompaktní právě tehdy, když obsahuje nejméně vazby v podobě dvojic.

Uváděli jsme si, že počet dvojic demonstrovaného příkladu BT(11) je 55. Z toho jednoduše dovodíme, že dvojice (SYMPTOMY) obsahují každý různý prvek signatury právě 5x. To je vzhledem k množině signatur problematické. Množina musí mít unikátní prvky. Ale také jsme si říkali, že dvojice kombinací jsou UNIKÁTNÍ VAZBY a hovoříme o SYMPTOMECH. A těchto unikátních symptomů je 55.

Existují – li všechny dvojice systému, potom existuje systém jako celek v unikátní [u]časové SOUČASNOSTI[/u]. Dá se předpokládat, že systém jako takový bude obsahovat i vyšší k – tice, ale jednice samy o sobě důkaz neposkytují.

Vysvětlíme si to na zkrácené verzi modelu her 6/49 tak jak je uvedeno výše.

1. Combin(49;0) = dvojice žádné
2. Combin(49;1) = dvojice žádné
3. Combin(49;2) = 1 dvojice
4. Combin(49;3) = 3 dvojice, 1 trojice
5. Combin(49;4) = 6 dvojic, 4 trojice, 1 čtyřčíslo
6. Combin(49;5) = 10 dvojic, 10 trojic, 5 čtyřčísel, 1 pětičíslo
7. Combin(49;6) = 15 dvojic, 20 trojic, 15 čtyřčísel, 6 pětičísel, 1 šestice

To co vidíme je nárůst k – tic. Důležité jsou celkem konstantní poměry výskytu, ale také velmi zřetelné stoupání počtu k – tic vlivem postupného přidávání jednic. Takové postupné přidávání už je určitým typem časové posloupnosti ačkoliv nevíme nic jiného nežli že kroky 1 až 7 postupně za sebou následovaly – nebyly SOUČASNÉ.

POZNÁMKA : Tedy žádný čas startu, ani rozpětí mezi jednotlivými přírůstky. Není ani nutné se zabývat zda intervaly mezi jednotlivými přírůstky byly „stejně dlouhé“. Konec nastal vhozením (vylosováním) posledního prvku. nevíme tedy zda stav setrvává, či nikoliv. Víme jistě jen to že měl přesný počet etap a že jeho vnitřní obsahy nerostly lineárně s přírůstkem po jedné. Šlo o kvalitativně – kvantitativní skoky. Tyto skoky jsou ale skutečně SOUČASNÉ.

Například mezi třídami 4. a 5. byla přidána jedna kulička (prvek) a naráz se změnil počet k – tic z [3 dvojice a 1 trojice] na [6 dvojic, 4 trojice, 1 čtyř-číslo]. Rozdíl je velice markantní + 3 dvojice, + 3 trojice, + 1 čtyř-číslo.

Proto stačí vyšetřit počet dvojic a dostaneme přehled o celém systému. Podáme si ještě jiný důkaz o významu matematického času.

DŮKAZ EXISTENCE MATEMATICKÉHO ČASU.

Mějme 2 nezávislé množiny kombinací :

M(a) = Combin(12;3) = 220

M(b) = Combin(4;1) = 4

Vidíme že nejsou stejné ale chtěli bychom je srovnat. Takže se pokusíme oba výsledky sečíst a vydělit dvěma. 220 + 4 = 224/2. To se rovná 112. Takový výsledek by měly dát stejné poloviny systému.

Totéž se pokusíme udělat i s oběma (n=12) a (n=4) tedy dohromady n = 16/2 = 8. Podobně (k=3) a (k=1) průměrně tedy 4/2 = 2.

Proto očekáváme výsledek 112 z kombinací 2. třídy celku 8. Ten ale dá ze vzorce Combin(8;2) výsledek 56. Takže oba stejné systémy dají dohromady pouze polovinu z celku 224.

Jedná se tedy o výraz C(12,3) + C(4,1) ≠ 2*C(8,2), ale ve skutečnosti C(12,3) + C(4,1) = 4*C(8,2). Ač se to jeví jak chce divně, nebo infantilně, tak obě půlky nejprve musí být součástí stejného systému a pak se dá rozdělovat. Sjednocení tedy musí být na SOUČASNÉM SYSTÉMU a nikoliv na dvou či více různých a nesoučasných systémech. Viz :

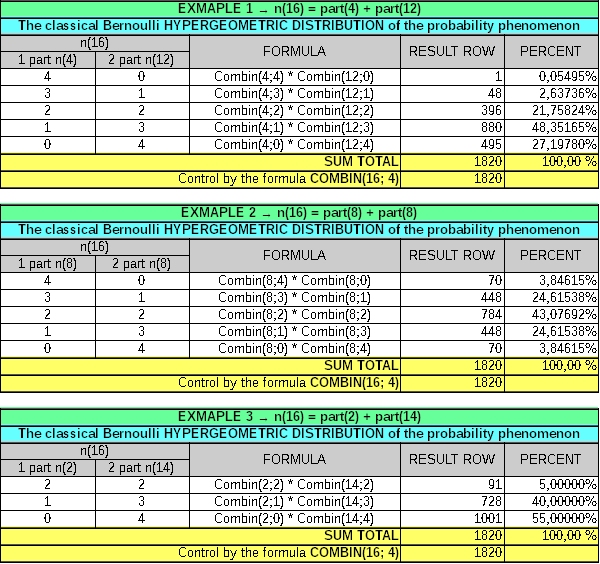
Teprve nyní můžeme posoudit skutečnost, že oba systémy množin musí být součástí jediného systému COMBIN(n1 + n2; k1 + k2).

Ve finále se jedná o nepochopení potenciálu množin kombinatorického typu. Je tedy jedno jestli hovoříme o kombinacích, variacích bez opakování, variací s opakováním, Partitio Numerorum a odvozených PERMUTACÍ.

Potenciálem je vždy výraz C(n,n). Ale okamžitě narážíme na problém. Například Permutace(n) = Variace(n,n) = Faktoriál(n). Toto je nebetyčný nesmysl. Zabývat se tímto problémem budeme v jiné kapitole.

Tato kapitola sleduje výrok, že postačují dvojice systému ke všem dalším operacím. Takže jedním důležitým rozměrem který musíme předem objasnit je absolutní nepochopení významu Pascalova trojúhelníku jako potenciálu obecných kombinatorických množin.

V každém řádku Pascalova trojúhelníku je vidět zřetelně, že pro každé (n) existuje potenciální (k)[0, 1, …., „n“]. Tedy od C(n,0), C(n,1), až C(n,n). Pro kombinace platí vztah že součet potenciálů (0,..,n) je roven 2^n. Ale výraz pro variace s opakováním není množinou. Nejdříve si ukážeme výpočtovou shodnost symptomů :

[u]Důvod je jednoduchý Množinou ve smyslu teorie množin i kombinatoriky (podmínka současnosti) jsou pouze systémy konstantního (n) a (k).[/u] Proto je každý řádek pouze potenciálem. Množinou je každý jednotlivý výraz z řádku protože jen tak může být množina SOUČASNÁ.

Na podporu tvrzení že dvojice postačují vždy a ve všech případech si ukážeme následující tabulku. Ta má mnohem více účelů ale k těm se vrátíme v jiných kapitolách :

V rámci této kapitoly nás zajímají pouze červeně označené buňky tabulky. Jednoduchým náhledem zjistíme, že buňky směrem vlevo nemohou vypovídat o systému nic jiného, nežli kolik má prvků. Z pohledu kombinací, variací bez opakování i u variací s opakováním je počet jednic shodný. U dvojic (tedy červeně podbarvených) je to jinak. Druhé třídy už shodné nejsou.

Právě z tohoto důvodu je jakýkoliv výpočetní systém schopen pracovat s typem C(n,2). Typy menší nemají výpovědní hodnotu a větší jsou už prakticky zbytečné.

Když je ve hře eso jménem Partitio Numerorum mohou se konat zázraky.

Nejlépe je si ukázat jak vypadá PN in natura. Tedy konkrétně PN(16)

Možná je divné proč na tomto místě uvádím obraz PN. Důvod to má. Výše jsme si ukázali :  Symptomatika dvojic na příkladu Pascalova trojúhelníku do třídy 16. Následně jsme si ukázali výpočtové potenciály právě na n(16) řádku Pascalova trojúhelníku Výpočtové potenciály – důkaz pro druhé třídy.

Proto si můžeme ozřejmit také to, že jsme použili k výpočtovým důkazům také příklady pro HYPERGEOMETRICKÉ ROZDĚLENÍ jevu pravděpodobnosti podle Bernouliho. Použili jsme pouze 3 případy z osmi možných PN(16,2).

Dvojice graficky.

Teprve nyní lze pochopit význam dvojic naplno. Grafický základ má mnoho aplikačních alternativ. Ukážeme si jen základní aplikace. Opět si ukážeme množinu 16 prvků. Musíme pochopit že nad touto množinou vládne PN(16) spolu s různými operacemi C(n,k).

Příklad 1 a 2

Pochopení matic a účely numerických analýz. Prvním příkladem je problém popsaný jako problém MATEMATICKÉHO ČASU ve formě podmíněné současnosti. Patří stejně jako druhý příklad do logického pracovního módu. Druhý příklad se zabývá rozkladem polynomu 4^4. Zde je spíš naznačeno použití v rámci algebry a to v obou příkladech. První příklad používá dvě množiny, ale jedna je označena numerickým znakem a druhá alfabetickým. U prvního příkladu je navíc znázorněna společná část jako zelený průsečík. Ve skutečnosti existuje tento pouze v případě sjednocení obou množin.

To co je zde naznačeno v prvním příkladu upozorňuje také na posloupnosti. Alfabeticky značená část by měla přirozeně numerické základy prvků od čísla 5 do čísla 16. Součet posloupnosti [5,..,16] je vidět na první pohled. Je to součet 12*4 + Combin(12;2).

Obecně tedy není potřeba řešit zda je počet čísel v posloupnosti sudý nebo lichý. Platí že posloupnost na úseku x1..x2 a y0..y2 je dána jako x2*y2 – Combin(x2-x1;2). Slovy : z obdélníku x*y odečteme dvojice Combin(x;2).

Další dva příklady jsou ukázkou práce v 2D grafickém módu. [u]Grafickým módem rozumíme typ deskriptivní geometrie[/u]. Přestože také logický mód je grafický. To je dáno nástrojem – průsečíkovým grafem ploch.

Třetí příklad se zabývá rozkladem pomocí řady (p=0)^2, (p+1)^2, (p+2)^2, (p+3)^2,….x^2. Čtvrtý příklad je ukázka použití PN(16) pro grafické rozklady. Zde je to provedeno pouze symbolicky, protože 2 různé členy mohou mít 2^2 uspořádání. Také je to ukázka jak pracovat s druhou odmocninou, respektive polovinou – což je vrchol jednotlivé třídy. Podobně je to vidět pro ostatní třídy PN(16).

Rozklady pomocí PN(16) mají celkem 231 řádků. PN(16) ale poskytuje vyčerpávající možnosti rozkladu. Na obrázku 4 vidíme základ 4^2 což je první třída. Také lze asi vyloučit několik posledních tříd, nebo posledních řádků tříd. Reálně bych tipoval, že se může používat cca 200 – 220 řádků počínaje řádkem 2 Připomeneme si PN(16) z obrázku tabulky.

ZÁVĚR TÉMATU

V další kapitole se budeme zabývat příklady obrazů 2D a 3D. Jedná se o jiné popisy nežli jsou v posledních čtyřech příkladech.

Teprve v další kapitole už můžeme efektivně využít informace z této a předchozí kapitoly. V této kapitole byly spíš jen navedeny témata a vzápětí odkázaná na jiné kapitoly. Právě z těch dalších kapitol budeme odkazovat zejména na tabulky z této práce, které jsou ve skutečnosti obrázky. Proto se musím omluvit za to, že tabulky jsou uvedeny v anglickém jazyce.

Běžný text umí přeložit WordPress, nebo překladač Google, ale obrázky by musely projít procesem OCR. Mimo toho jsem musel dbát na to, aby skutečně pomocí rekurzivních překladů text vyzněl tak jak jsem zamýšlel. Překladače většinou napoprvé vydají nesprávný překlad, ale ani další překlady často nevyhovují. Proto jsem mnoho původních českých popisů zcela přepracoval.