Klasický algoritmus kombinací

Princip rozložení limit a pracovního prostoru

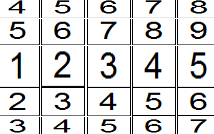
Obrázek nám ukazuje pracovní prostor (modrý) ohraničený horními limitami (žluté) a dolními limitami (zelené). Zajímá nás graf jako „schodiště“ – tedy jen buňky s červenými rámečky. Použijeme přirovnání k terminologii z oblasti stavebnictví. V tomto našem případě je to schodiště podobné s prefabrikovanou schodnicí, nebo lépe stupňům s jednostranným vetknutím (krakorec), a nebo jako shora zavěšené lehké chody. Je to proto, že vidíme výšku pomyslného nosníku (schodu) z boku (T1-Tk). (Například faktoriál a variace bez opakování vypadají jako schodiště s vlastní nosnou zdí založenou do roviny (základu). Variace s opakováním vůbec jako schody nevypadají (blok AxB). Parmutace mohou být na všechny možné způsoby – například jako variace, ale za schodem 1 hned schod 5, pak schod 12 a nakonec třeba i schod 3. Také může kombinavoat zavěšené schody s těmi, které mají vlastní nosnou zeď.)
Na obrázku jsou vyznačeny jednotlivé sloupce jako T1 – T5. Jsou tím myšleny jen limity jednotlivých sloupců T1(limita dolní, limita horní), , , , T5(limita dolní, limita horní). Ty jsou totiž společné ůplně pro všechny kombinace 5. třídy C(n,5), nebo lépe T1 – Tk a nejen pro obecnou třídu kombinací, ale všech kombinatorických pojmů (tedy kombinace, variace, faktoriál a permutace). Nerozhoduje jak je n veliké. Pokud hovoříme o konkrétním n, pak bychom užívali místo písmene „T“ písmeno „R“. Potom T (jako Turniket) je ohraničení pro R (jako Registr). Tím vysvětluji symboly použité dále v textu.
Názorně příklad pro T a R systému kombinací C(9,5)
T1 = [1,5] R1 = [1,2,3,4,5]
T2 = [2,6] R2 = [2,3,4,5,6]
………………….
T5 = [5,9] R5 = [5,6,7,8,9]

Jiným případem jsou pojmy „limit T1″ ….“limit T5“

Jsou to součtové limity pro generátory Názorně je to provedeno ve spodní části obrázku. Například Spodní limity pro Tx jsou limity startovní, a používají se jen někdy na začátku. Proto pod Tx prakticky výlučně rozumíme horní limitu registru Rx. Generátor může sice vyjádřit podmínku pro R1 například T2+T3+ + Tx, ale techničtější je deklarovat limitu pro R1 jako SUM(T2….Tk). Práve tohle je lim(Tx). Pokud hovoříme o T(lim) měla by u toho být ještě šipka, ale protože jde převážně jen o horní limitu, označíme šipkou jen limitu dolní. Například T(↓).

Princip fungování jako „tachometr“ se speciálním řazením (posuvem).

Speciální řazení vychází z toho, že změna na registru vlevo zapůsobí na všechny registry vpravo konkrétně pro demonstarční množinu C(9,5):

R5 (poslední registr na pravé straně – proto nic směrem doprava neovlivní)
R4 = R4+1 (předposlední registr na pravé straně) – ovlivní nastavení R5 = R4 + 2 (viz poznámka)
R3 = R3+1 (prostřední registr) – ovlivní nastavení
R4 = R3 + 2, R5 = R3 + 3 (viz poznámka)
R2 = R2+1 (druhý registr na levé straně) – ovlivní nastavení R3 = R2 + 2, R4 = R2 + 3, R5 = R2 + 4 (viz poznámka)
R1 = R1+1 (první registr na levé straně) – ovlivní nastavení R2 = R1 + 2, R3 = R1 + 3, R4 = R1 + 4, R5 = R1 + 5 (viz poznámka)
Poznámka :
Algoritmus v této podobě platí jen pro některé rekurzivní algoritmy. Konkrétně pro vzorce tabulkových procesorů. Může, ale také nemusí platit pro rekurzivní algoritmy obecně.
Jedná se o to, jakou má algoritmus sémantiku.
– Pokud načítá nové hodnoty do proměnných které užije ke zpětnému dotazu, tak platí dříve popsaný algoritmus také.
– Pokud však přestavuje hodnoty načítáním hodnot nově vzniklých, připočítává například takto :
R4 = R4 + 1, R5 = R4 + 1 (Modrá = nová hodnota R4 -/- červená = původní R4, R5)
Zde se možnosti opět větví. Vysvětlíme to na registrech R1 :
A: R1=R1+1, R2=R1+1, R3=R1+2, R4=R1+3, R5=R1+4
B: R1=R1+1, R2=R1+1, R3=R2+1, R4=R3+1, R5=R4+1
– Je zřejmé, že asi nejvhodnější je úplně první způsob pro všechny rekurzivní algoritmy kombinací. Ale může vzniknout požadavek na redukci kódu a pak by zřejmě došlo na některý ze způsobů A, B.

Obraz průběhu generování – zvýraznění vstupu T (turniketů)

Jak název napovídá, ukazuje obrázek kdy a které limity „zafungují“. Jde samozřejmě jen o několik prvních k-tic (řádků).
Barva zelená : spodní limity
Barva žlutá : horní limity
Barva modrá : střední hodnoty

Pozor! Naznačený postup je poplatný pouze lexikálním generátorům. Existuje poměrně mnoho generátorů, které nejsou lexikální.
Poznámka :
Výraz „lexikální“ je odvozen od rejstříků užívaných pro textové soubory. Správně bych měl napsat „pro knižní“, nebo jiné podobné „textové“ práce větších rozsahů. Jde o alfabetické třídění podle znaků jdoucích za sebou. Tedy 1. znak udává místo ve sloupci výrazů stejného znaku. Následně také podle délky řetězce (pro nás je to k). Jde tedy o systematiku třídění vzestupně zleva doprava a shora dolů. Následuje pořadí podle druhého a každého dalšího znaku. Ale tohle by měl znát každý velice důvěrně (pokud někdy něco odborného četl 🙂  ). Tyto rejstříky mají také před jednotlivá písmena upřednostněna čísla. Ale řazení je textové. Takže například 1,11,111 předchází před 2,21,22 ..následuje 3,30,31.. a tak dál. Tím ale nevylučuji možnost, že některé rejstříky pro oblast čísel použijí řazení číselné – decimální. Pokud tedy hovoříme o lexikálním řazení dáváme pozor, aby skutečný význam nekolidoval s decimálním řazením čísel. Například zrovna pro kombinace stejné třídy (nejspíš zápis UV) by ke kolizi nedošlo. Naopak pokud existují jen číselné výrazy, pak bych si dovolil tvrdit, že řazení decimální (obecně číselné podle velikosti – například formát hexadecimální, osmičkový ap.) je validnější nežli typicky textové řazení a dá se spolu s ním také použít ve stejném smyslu slova. Věcně se jedná jen o to, že existuje potřeba prohledávat „stromy“. Známější jsou stromy binární, ale lepší na prohledání jsou stromy lexikální. Právě například kombinace jsou typem stejně vhodným, ne li vhodnějším pro procházení stromových struktur nežli lexikální uspořádání. Samozřejmě za předpokladu, že celý strom je „kombinační“. Podrobně se tímto zabýváme v Teorii kombinatoriky Kombinatorický strom.
Já nemám rád takové algoritmy, které nejsou lexikální. Ale svůj omezený význam mají zejména pro šifrování. Jinak se ale nehodí naprosto k ničemu.

Některé rozhodující přechody – popis funkcí limit.

Názorné dokreslení toho jak limity řídí iterace, nebo také „tachometr“. Poslední řádek (2×2 grafy) zobrazují funkci ukončení algoritmu. Dvojice grafů vlevo reprezentuje neuzavřený cyklus. Takový algoritmus po poslední k-tici (poslední řádek) vygeneruje řádek první – startovní.

Uživatelé mohou preferovat algoritmus s ukončením. To reprezentují dva grafy vpravo. (V takovém případě doporučuji buď další předřazenou podmínku, nebo jen místo startovní hodnoty zadat nějaké písmeno. Výsledkem vzorce je nejprve zobrazení řádku písmenem (v grafu jsem použil „E“). Potom následuje už jen oznámení chyby (číslo) ze strany systému.

Pokud vnoříme další dotaz, může se například za posledním řádkem opakovat stále stejná fráze. To platí zejména pro vzorce tabulkových procesorů, které se kopírují ručně. U programovaných generátorů předpokládáme, že taková situace vzniknout nemůže.)

Skládaný algoritmus kombinací

To je poněkud odlišný náhled jako návod pro konstrukci kombinací. Je však pravděpodobné, že některým lidem utkví v paměti snáz, nežli předchozí popisy s grafickým, nebo klasickým popisem. Neopírá se totiž o čísla, ale o obecné označení. Pro demonstraci jsem zvolil typ označení barvou pozadí. Pro jednoduchost budeme skládat všechny třídy kombinací z celkového počtu 5 prvků.

Utvoření 1. třídy kombinací celku 5 prvků C(5,1)

První třída se vytváří z třídy nulté, tu si ale znázorňovat nebudeme. Bylo by to na tomto místě nelogické. Odradilo by to možná i jinak velice vnímavého uživatele.

Představíme si, že potřebujeme postavit systém 5 prvků. Proto si nejprve vytvoříme očíslovaný sloupec od 1 do 5. Následně místo čísel použijeme barvy (a pomocné šipky vyjadřující vzestupné uspořádání. Orientace šipek je možná na první pohled nelogická. Má to důvod v tom jak vznikají třídy kombinací z nulté třídy. Přidává se vždy větší číslo na konec sloupce. Právě tohle symbolizují šipky.).

Utvoření 2. třídy kombinací celku 5 prvků C(5,2)

Obrázek opět nejprve na formátu s čísly ukazuje jak proběhne skládání. Nejprve tedy ze systému jednic C(5,1) odebereme číslo 1 a předřadíme ho všem ostatním jednicím. vznikne
z [1,2,3,4,5] → [12,13,14,15]
To jsou všechny dvojice s jedničkou na začátku. Popisuje to první sloupec obrázku s označením (+1). V dolní části už zůstávají jen barvy (místo čísel) a šipky jako symbol řazení.
Následují všechny dvojice začínající číslem 2. Proto je původní [1,2,3,4,5] zredukováno na [1,2,3,4,5] = [2,3,4,5] a postup je podobný :
z [2,3,4,5] → [23,24,25]
To nám ukazuje sloupec s číslem (+2). V dolní části jsou už opět jen barvy a šipky.
Následují všechny dvojice začínající číslem 3. Proto je původní [2,3,4,5] zredukováno na [2,3,4,5] = [3,4,5] a postup je podobný :
z [3,4,5] → [34,35]
Nakonec zbývá dvojice začínající číslem 4. Proto je původní [3,4,5] zredukováno na [3,4,5] = [4,5] a postup je podobný :
z [4,5] → [45]

Dostáváme výsledek:
12 = výsledek ze sloupce (+1)
13 = výsledek ze sloupce (+1)
14 = výsledek ze sloupce (+1)
15 = výsledek ze sloupce (+1)
23 = výsledek ze sloupce (+2)
24 = výsledek ze sloupce (+2)
25 = výsledek ze sloupce (+2)
34 = výsledek ze sloupce (+3)
35 = výsledek ze sloupce (+3)
45 = výsledek ze sloupce (+4)

Utvoření 3. třídy kombinací celku 5 prvků C(5,3)

Postupujeme zase podobně jako v předchozím případě. Použijeme ale jiný popis postupu, aby bylo jisté, že byl princip pochopen. Nejprve tedy ukážeme obrázek schematicky shodný s tím, který je vložen k odstavci o tvorbě dvojic. Následovat bude jen odlišný popis postupu :

Na obrázku již nejsou vykresleny šipky. To má svůj důvod. Můžeme však poznamenat, že už víme oč se jedná. Šipky nám posloužili výborně v případě tvorby C(5,1) a C(5,2). Správné zobrazení šipek na této množině by bylo matoucí. Šipky se nám pochopitelně ještě objeví u systému C(5,4) a C(5,5), ale mají jinou orientaci. Názorný algoritmus pro tvorbu C(5,3) : –
12 eliminace
13 eliminace
14 eliminace
15 eliminace
23 akceptace + 1 = 123
24 akceptace + 1 = 124
25 akceptace + 1 = 125
34 akceptace + 1 = 134
35 akceptace + 1 = 135
45 akceptace + 1 = 145
————————————————-
23 eliminace
24 eliminace
25 eliminace
34 akceptace + 2 = 234
35 akceptace + 2 = 235
45 akceptace + 2 = 245
————————————————-
34 eliminace
35 eliminace
45 akceptace + 3 = 345
Myslím, že tato demonstrace je opravdu názorná. Proto budeme pokračovat stejným stylem i pro vytvoření třídy C(5,4).

Utvoření 4. třídy kombinací celku 5 prvků C(5,4)

Nejprve ukážeme obrázek shodný s původní logikou. Myslím, že logika je už celkem zřejmá. Ale upozorníme na to, že se nám zde objevily znovu šipky. Nyní už ale neukazují jen směr třídění vzestupně (směr růstu velikosti) ve sloupci, ale v řádku.

Postup byl uveden výše, takže bez komentáře:-
123 eliminace
124 eliminace
125 eliminace
134 eliminace
135 eliminace
145 eliminace
234 akceptace + 1 = 1234
235 akceptace + 1 = 1235
245 akceptace + 1 = 1245
345 akceptace + 1 = 1345
—————————————————
234 eliminace
235 eliminace
245 eliminace
345 akceptace + 2 = 2345

Utvoření 5. třídy kombinací celku 5 prvků C(5,5)

Zde už také není ani co komentovat:
1234 eliminace
1235 eliminace
1245 eliminace
[1345 eliminace
2345 akceptace+ 1 = 12345

Souhrn výsledků Pascalovy třídy kombinací 2^5

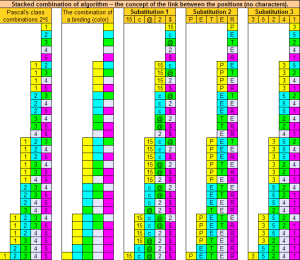
A: – 1 sloupec reprezentuje souhrn všech postupů počínaje C(5,1) až k C(5,5). Uvádím sice, že je to celá Pascalova třída 2^5, ale schází tam nultá třída, tedy C(5,0). Jak jsme se k tomu dopracovali je doufám zřejmé. Vůbec nic se nemusí počítat. Stačí přidávat jen znaky na správná místa. Je to postup opravdu grafický. Není vypočítávaný. Je jen sestavovaný logicky – skládáním. A tenhle atribut je pro pochopení Teorie kombinatoriky téměř rozhodující. Kombinace, ale i variace a faktoriál jsou výhradně logickou záležitostí. Ale tohle samozřejmě není určující důkaz pro novou axiomatizaci. K dispozici je několik opravdu validních důkazů.
– Přestože jde jen o skládání, lze velice dobře algoritmus popsat v programu. Je možné sestrojit jak iterativní, tak rekurzivní verzi. Navíc takové algoritmy nejsou limitované třídou k, nebo počtem možných n – na rozdíl od těch které popisuji v ostatních kapitolách.

B: – 2 sloupec demonstruje už jen vazby pomocí barev. Snadno si představíme, že barvy nejsou čtverečky z tabulky, ale barevné hrací kuličky. Velice rád bych napsal, že prvky kombinatorických množin jsou uzavřené intervaly na oboru čísel N..[0,1,2,…,n]. To ale nemohu hned ze dvou důvodů. Logika podléhá výlučně definici Euklidovi číselné osy a jejím prvkům. Do důsledku to znamená, že prvky jsou stejně vnitřně rozměrné jako prvky Euklidovy číselné osy – nemají žádný vnitřní rozměr. Jejich rozměrem je jen vnější vzdálenost od počáteční nuly (interval). Tento vnější rozměr vyjadřujeme pořadím – a to nám zde demonstrují nejlépe příklady substitucí. Tedy všechny 3 sloupce na pravé straně. Ten druhý důvod je právě v tom, že pořadí je dáno jen relativní pozicí a konvencí, že první pozice je právě první „barva“ z levé strany, nebo shora.
Ovšem doslova to znamená, že na některé pozici kombinavaných prvků bude například písnička (- úložiště na HDD – MP3). Na jiné pozici bude odkaz kde mám večeři (papír s poznámkou na lednici), a jiný podobný – kde mám kalhoty a peníze (telefonické info). Poslední je rozkaz – vynes koš (automatická činnost). Já mimo toho svobodomyslně rozhodnu, že půjdu na pivo.
Rozhodnu se pro postup teprve v okamžiku, který mi nejvíce vyhovuje. Například si poustím písničku (při tom se najím) následně zvolím kombinaci kalhoty – peníze – odpadky a restaurace. Stejnou volbu mám druhý den, ale pořadí bude jiné. Přes to jde stále o stejné kombinace. Mohu například zvolit postup jen kalhoty – peníze – restaurace, ale budu hladový a manželka mne roztrhne jako hada, protože jsem nevynesl koš.
To jsou také kombinace a řešíme je každý den znovu dokola. Je jich asi víc, ale počet n,k je dán pokaždé jinak. Ovšem všechny se dají sumarizovat jako největší možné n od C(n,k(0..n)). Tedy jako stále stejná třída 2^n. Nic se na ní nezmění. Rozhodující je jen právě počet n. Pořadí je jako ponožky – stále se střídá. Ale kombinace jsou konstantní. Vysvětlení je na 4. a 5. sloupci. To jsem si nechal na závěr.
Poznámka :
Aritmetika s prvky bez vnitřního rozměru je velice fádní. p1+p3 = 0, stejně jako p3-p1, nebo p1-p3. Podobně všechny operace pokud jsou definovány.
Úplně jiný případ nastává, pokud Existuje n > 0. Potom existují prvky a jejich intervaly, ale mají vnitřní rozměr „1“ buď p=0^0, nebo p=0^1. To už je barvitější počítání. Například 5+9 = 2, nebo 5*9 = 1. Samozřejmě 4-9 = 0 stejně jako 9-5 = 0. Teprve když interval prvku i(p) ≡ p^1 můžeme používat vlastní vnitřní velikost čísla a dovolávat se logiky, že to vychází z jeho intervalu. 🙂

C: – 3 sloupec demonstruje substituci – což je vlastně konkretizace prvku. Demonstrace spočívá v tom, že prvky jsou poskládány do kombinací a například s čísly to nemá nic společného. Mohou to být klidně třeba hrací karty, nebo cokoliv – náhodně a bez setřídění. Přes to jsou „vytvořeny“ všechny kombinace vždy stejně. Nyní je čas na otázku – co jsou kombinace? Ano zřejmě jen „množina“. Ale jaké jsou její typické znaky? Je možné tvrdit, že je to „uspořádání“ – ale jaké? V čem to typické uspořádání spočívá? – Samozřejmě tato otázky se pokouším řešit v Teorii kombinatoriky, ale Vy se podívejte jak „kombinace“ definují jiní autoři.Záver grafických algoritmů kombinací.

Na závěr kapitoly jsem si nechal vysvětlení významu sloupců 4. (substituce 2) a 5. (substituce 3)

D: – 4 sloupec (substituce 2) nám demonstruje něco, co by do kombinací bez opakování patřit nemělo. Barevné podklady jasně ukazují, že se jedná o kombinace. Ty jsme vytvořili skládáním, ale bylo by jedno jak byly utvořeny. Nepochybujeme o tom, že to jsou kombinace bez opakování. Přes to je substituce provedena jménem PETER, které obsahuje 2 stejné znaky. Vzniká teoretické dilema. Jsou to kombinace s opakováním, nebo ne? Samozřejmě nejsou. Není to ani protimluv v rámci mých výroků. Kombinace s opakováním skutečně neexistují ve formě té oficiálně uznávané, a ani ve formě substituce do systému kombinací bez opakování. Vše je dáno jen pozičním uspořádáním, ne stejnojmenným označením prvků. p1(P), p2(E), p3(T), p4(E) a p5(R). Můžeme to zjednodušit 1=P, 2=E, 3=T, 4=E, 5=R. Nebo 1(p), 2(e), 3(t), 4(e), 5(r). Je úplně jedno zda : 4(p), 5(e), 2(t), 1(e), 3(r). Pak je teprve zřejmé, že 2(e) ≠ 4(e), ani 5(e) ≠ 1(e). Vlastní znak úlohu nehraje. Hraje úlohu pozice. Ty mohou být zamíchány jak libo, ale neexistuje shodnost dvou pozic množiny.

E: – 5 sloupec nám poslouží k důkazu, že jakákoliv substituce striktně kopíruje základní vazby kombinací. Znamená to, že každou substituci můžeme pomocí třídění upravit na standardní (normalizovaný) tvar původního modelu (Platí to také pro všechny ostatní kombinatorické pojmy – variace, permutace a tak podobně).
A ještě je tu jedna maličkost, která není na první pohled zřetelná. Poziční uspořádání je typické jen třídě výběru (k).. Každé poziční uspořádání prvku lze cyklicky změnit, ale tuto vlastnost mají všechny prvky shodnou. Každý různý prvek na stejné pozici utvoří stejné uspořádání jako jiný prvek na jeho pozici.Obrázek na závěr a bez komentáře :