Polynomy

V rámci dvojčlenů (binomů) je představa poměrně jednoduchá zejména když víme, že řešením bude kvadratická rovnice buď (a + b)², nebo (a – b)². Roznásobíme buď :

(a + b)(a + b) názorně roznásobením a(a + b) + b(a + b) = a² + ab + ab + b² = a² + 2ab + b².

Nebo v jiném případě :

(a – b)(a – b) názorně roznásobením a(a – b) – b(a – b) = a² – ab – ab + b² = a² – 2ab + b².

Rozklady :

Typické je zpětné rozložení například pro tvar a² − b² = (a + b)(a − b), které používáme při řešení kvadratických rovnic.

Obrázek nám znázorňuje grafickou reprezentaci typickou pro rozklad a² − b². Pokud bychom potřebovali graficky vyjádřit (a + b)², byly by oba členy ab kladné. V případě, že bychom potřebovali vyjádřit (a – b)², byly by oba členy ab záporné.

Poněkud obtížnější je představa u kubických rovnic. Graficky si vypomůžeme derivací, ale nejprve názorný polynom a rozklad :

(a + b)³ = a³ + 3a²b + 3ab² + b³, což je výsledek roznásobení (a + b)(a + b)(a + b), nebo

(a − b)³ = a³ − 3a²b + 3ab² − b³, což je výsledek roznásobení (a − b)(a − b)(a − b).

Rozklady :

a³ − b³ = (a − b)(a² + ab + b²), po roznásobení závorek a³ + a²b + ab² – a²b – ab² – b³,

a³ + b³ = (a + b)(a² − ab + b²), po roznásobení závorek a³ – a²b + ab² + a²b – ab² + b³ .

Graficky to lze znázornit poměrně obtížně ale v obou případech se střední členy navzájem krátí. Zbudou jen dva tvary buď a³ + b³, nebo a³ – b³. Graf by měl být prostorový. Graf nám ale nyní znázorňuje nikoliv rozklad, ale polynom (a + b)³, nebo (a − b)³.

Z obecnějšího pohledu lze plochu vyjádřit buď jako odmocninu, tady vstupem do grafu bude čtverec, ale skutečná plocha nemusí být čtvercem. Například rozměr a = r*s (r ≠ s), b = t*u (t ≠ u) nám umožňuje skutečné zobrazení ploch, ale to má více variant. Například v ose x(r,t), v ose y(s,u), nebo x(r,u), y(s,t), x(s,u), y(r,t), bez změny pozic objektů (a, b) 2² = 4 různá zobrazení. Při akceptování různých pozic objektů (a, b), nebo (b, a) 2³ = 8 různých zobrazení. Při řešení kvadratických rovnic nás to musí zajímat stejně jako směrnice (přepona) objektů a podobně.

V případě prostorových objektů je to ještě složitější. Když ale potřebujeme řešení, vypomůžeme si schematem, které používá pouze maximálně členy s druhými mocninami. Je to kompromis, ale někomu to může pomoci.

Vycházíme z jednoduché derivace. Například pro (a³)´ = 3(a²), respektive ((a+b)³)´ = 3(a+b)². Podobně v případě rozkladu (a³)´+ (b³)´ = 3a² +3b². Podobně si vypomůžeme u vyšších mocnin a polynomů vyššího řádu tak abychom získali nejvýše druhé mocniny.

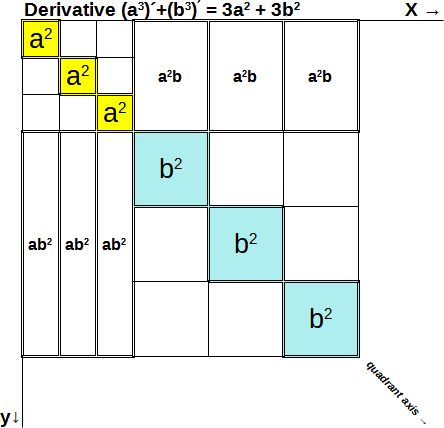Není to ideální zobrazení vzhledem ke tvaru binomu (a + b)³ = a³ + 3a²b + 3ab² + b³, respektive ani k rozkladu a³ + b³ = a³ – a²b + ab² + a²b – ab² + b³. Ale v případě binomu je lepší asociace představy pro tvary 3(a²b) a 3(ab²) i když a³ ≠ 3a², a stejně tak b³ ≠ 3b².